我们都知道一句话:鸡蛋不要放在一个篮子里。通常我们都是从安全角度去理解这句话,知道通过分散投资来降低风险。
关于分散投资,诺贝尔经济学奖得主哈里•马科维茨也有一句名言:“资产配置多元化是投资的唯一免费午餐。”既然是能吃的午餐,说明分散投资不仅仅可以降低风险,也能提高收益。接下来就从数学角度证明,仅仅通过把资产从全仓一种资产改为分散投资多种资产,不必承担额外的风险,就能收获更高的收益率。
为了简化问题,先做两个假设。
1,市场上有无数多的投资品,这些投资品每年的涨跌幅只有两种可能性,一半的可能性是涨40%,一半的可能性是跌20%。
2,投资者无法预判具体投资品未来一年的涨跌。
如果投资者总是全仓一个投资品,从概率上看,一半的年份收益是40%,一半的年份收益是-20%,长期年化收益率是5.83%。
[(1-20%)*(1+40%)]^(1/2)=1.0583
如果投资者每年投资两个投资品,且每年重新平均分配一次资金,从概率上看,投资者的收益每四年中有一年是-20%,两年是10%,一年是40%,长期年化收益率是7.89%。
[(1-20%)**(1+10%)*(1+10%)*(1+40%)]^(1/4) = 1.0789
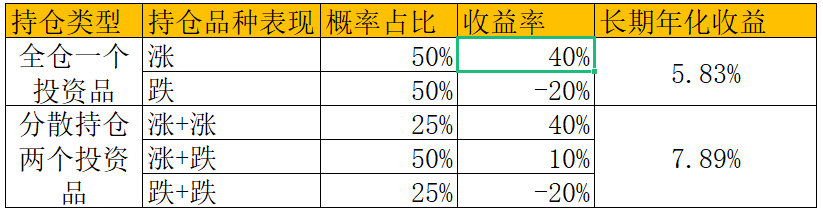
可以看出,同一个投资者,同一批投资品种,仅仅通过分散持有两个投资品种、每年重新平衡一次资金,无需承担额外风险,就能把收益率提高两个百分点。
如果投资者有一定的预判能力,可以有较高概率选择到上涨的投资品,分散投资是否也能提高投资收益呢。先来两个假设。
1,市场上有无数多的投资品,这些投资品每年的涨跌幅只有两种可能性,一半的可能性是涨40%,一半的可能性是跌20%。
2,投资者主动选择未来会上涨的投资品,有2/3的成功概率。即每选择三次,选到上涨者两次,选到下跌者一次。
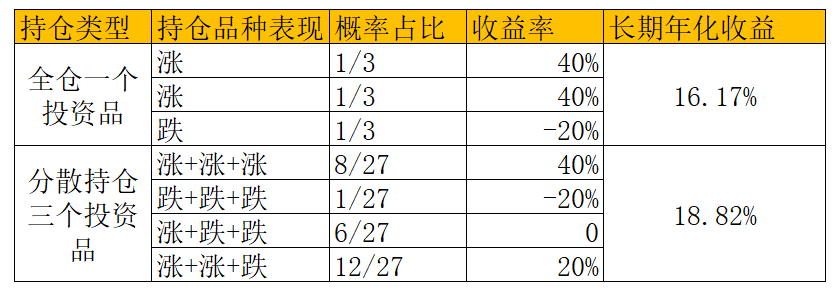
分散持仓年化收益的计算如下:
[0.8*1*1.4^8*1.2^12]^(1/27) = 1.1882
可以看出,有预判行情能力的投资者,一样可以通过分散持仓、定期平衡资金的方式,无需承担额外风险就能提高收益。
图2中分散持仓各种情形的概率占比计算,可以参考如下模型。
关于分散投资,诺贝尔经济学奖得主哈里•马科维茨也有一句名言:“资产配置多元化是投资的唯一免费午餐。”既然是能吃的午餐,说明分散投资不仅仅可以降低风险,也能提高收益。接下来就从数学角度证明,仅仅通过把资产从全仓一种资产改为分散投资多种资产,不必承担额外的风险,就能收获更高的收益率。
为了简化问题,先做两个假设。
1,市场上有无数多的投资品,这些投资品每年的涨跌幅只有两种可能性,一半的可能性是涨40%,一半的可能性是跌20%。
2,投资者无法预判具体投资品未来一年的涨跌。
如果投资者总是全仓一个投资品,从概率上看,一半的年份收益是40%,一半的年份收益是-20%,长期年化收益率是5.83%。
[(1-20%)*(1+40%)]^(1/2)=1.0583
如果投资者每年投资两个投资品,且每年重新平均分配一次资金,从概率上看,投资者的收益每四年中有一年是-20%,两年是10%,一年是40%,长期年化收益率是7.89%。
[(1-20%)**(1+10%)*(1+10%)*(1+40%)]^(1/4) = 1.0789

可以看出,同一个投资者,同一批投资品种,仅仅通过分散持有两个投资品种、每年重新平衡一次资金,无需承担额外风险,就能把收益率提高两个百分点。
如果投资者有一定的预判能力,可以有较高概率选择到上涨的投资品,分散投资是否也能提高投资收益呢。先来两个假设。
1,市场上有无数多的投资品,这些投资品每年的涨跌幅只有两种可能性,一半的可能性是涨40%,一半的可能性是跌20%。
2,投资者主动选择未来会上涨的投资品,有2/3的成功概率。即每选择三次,选到上涨者两次,选到下跌者一次。
分散持仓年化收益的计算如下:
[0.8*1*1.4^8*1.2^12]^(1/27) = 1.1882
可以看出,有预判行情能力的投资者,一样可以通过分散持仓、定期平衡资金的方式,无需承担额外风险就能提高收益。
图2中分散持仓各种情形的概率占比计算,可以参考如下模型。
0
被忽悠傻的。你的两个计算都是错的。概率不能按时间摊开的。如果可以,那我投一个产品,投2年,按你的算法也是有四种可能,然后我把这四种可能分配到四个两年里(注意就是这一步错了),再连乘,再开四次根号。出来的结果必然和你的结果不同。那么问题来了,正确的算法,怎么可以算出2种年化收益率呢?
26
账户已注销
 - 过去发生的频率不代表未来发生的概率。
- 过去发生的频率不代表未来发生的概率。
赞同来自: YYF30 、款特长 、你猜再猜 、西风不瘦 、神经牛 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、更多 »
分散的收益和意义我借用下@brainzhang 的历史回帖。
根据楼主的例子再简化一下场景:
假设在牛市中,投一个股有50%概率所有本金亏-50元,50%概率赢100元,那么,只买一只股的期望收益是:(这里都假设所有股的盈利概率都是一样的性质)
单股:
0.5 *(-50) + 0.5 * 100 = -25 + 50 = 25 元
买两只股:
0.25 *(-50) + 0.5*(-25 + 50)+ 0.25 * 100 = -12.5 + 12.5 + 25 = 25 元
买三只股
0.125*(-50) + 0.375 * (-16.66 - 16.66 + 33) + 0.375*(-16.66 + 33 + 33) + 0.125*(100) = 25元
我们发现,买多只股并不会使期望收益增加,但在公式中最左边项的最坏收益-50元出现的机率逐步降低,在单股的时候为50%,双股25%,三股12.5%,最坏情况在以指数速度下降。也就是说分散投资有效降低最大回撤;
所以说组合投资是取得同样收益,同时大幅降低风险的免费午餐。
它不一定能使最终收益提高,但往往能降低极端风险。
所以桥水达里奥对我而言最有价值的话就是:投资的圣杯就是能够找到10-15个互不相关的回报流,互不相关很重要。
根据楼主的例子再简化一下场景:
假设在牛市中,投一个股有50%概率所有本金亏-50元,50%概率赢100元,那么,只买一只股的期望收益是:(这里都假设所有股的盈利概率都是一样的性质)
单股:
0.5 *(-50) + 0.5 * 100 = -25 + 50 = 25 元
买两只股:
0.25 *(-50) + 0.5*(-25 + 50)+ 0.25 * 100 = -12.5 + 12.5 + 25 = 25 元
买三只股
0.125*(-50) + 0.375 * (-16.66 - 16.66 + 33) + 0.375*(-16.66 + 33 + 33) + 0.125*(100) = 25元
我们发现,买多只股并不会使期望收益增加,但在公式中最左边项的最坏收益-50元出现的机率逐步降低,在单股的时候为50%,双股25%,三股12.5%,最坏情况在以指数速度下降。也就是说分散投资有效降低最大回撤;
所以说组合投资是取得同样收益,同时大幅降低风险的免费午餐。
它不一定能使最终收益提高,但往往能降低极端风险。
所以桥水达里奥对我而言最有价值的话就是:投资的圣杯就是能够找到10-15个互不相关的回报流,互不相关很重要。
 Edge
Edge Chrome
Chrome Firefox
Firefox

 京公网安备 11010802031449号
京公网安备 11010802031449号