Edge
Chrome
Firefox
读前须知
1，原文作者是Reddit期权板块的AlphaGiveth，全部内容由本人翻译，创作不易，如需转载请注明出处。2，本人也是期权新手，对文章内容正确性不做保证。
3，Reddit是外网一个著名的民间论坛，内容涉及方方面面，其子版块Wall Street Bets发起了去年韭菜反杀华尔街的著名“游戏驿站”事件。
4，本指南目前依然在更新之中，截止到今天原作者已经更新了13章，翻译工作量较大，我争取每天翻译一个章节。
5，美股期权与国内有诸多不同，比如美式期权可能提前被行权，比如美股的个股期权非常丰富等等，很多经验是相通的但也不可完全照搬。
6，其他章节链接在本文末尾。
第一章：期权卖方的盈亏之道
第一节：Theta是期权的一个属性让我们首先想象一下你想将自己的房子出租给路人甲，你会跟路人甲说：我的房子有三个卧室，两个洗手间，友善的邻居，房租是2000美元/月。
你提到的每个因素决定这个房子的好与坏，但你不能说因为你的房子有卧室或厕所，所以你的房子就比较好。
同样的，在期权中，theta，gamma，vega，delta等都是期权的属性。他们本身没有好坏之分，他们只是告诉你面前这张期权合约的特征。
第二节：把Theta想象成租金
如果期权是房子，那么theta就是租金，租客付了租金他们就拥有了进入使用房屋的权利。
在期权的世界里，买方付出了theta，他就可以得到使用期权的权利，那么你能答出买方付出了theta到底得到了什么吗？
第三节：路人甲的theta是路人乙的gamma
如果你的答案是gamma，那么恭喜你答对了。期权买家支付theta来获得gamma。
理解gamma的简单方式是它是期权对于价格变动的敏感程度。如果股价剧烈波动，那么买家会因为gamma挣到很多很多钱，对吧？那么为什么会有人愿意做卖家呢？
第四节：theta的大小与gamma风险高度相关
让我们回到房屋的例子，如果你想在纽约市中心租一间顶层复式，它的租金必然是非常昂贵的，因为你付出的租金可以换来很多绝妙的体验。如果它只租500美元/月，那么没有人会出租它，因此租金是与房子本身的属性相关的。
在期权的世界中，如果一只股票有很多的gamma风险，或者说股价具有较大的波动的可能，那么这只股票的期权所包含的theta也会比较多。因为如果theta不足以弥补gamma的风险，则没有人会做这个期权的卖方，那么交易也就不存在了。
现在关键点来了，在一个完全有效市场中，gamma风险由theta完全补偿，那么无论你做买家或者卖家都无法赚到任何钱。在这理想世界中，期权的波动风险可以由theta完全对冲。
因此，在现实世界中，期权价格里包含了一个“可变风险溢价”。
第五节：期权卖方因为承担了凸性风险而获得一个风险补偿
这个可变的风险补偿给了期权卖方一点小小的优势，作为他们承担股价大幅波动的补偿。
因为这个小优势，卖出期权是可以获得利润的。长期来看，你会有很多次小的获利，偶尔一次大的亏损。这就是我们所说的：做空波动率策略。
你可以观察股票的风险溢价。一个简单的方法是把期权的30日隐波与股票30日真实波动放在一张图上作比较。你可以观察到，隐波绝大多数时刻都高于真实波动，而两者之差就是风险补偿。你也可以观察到在一些短暂的区间里，真实波动上涨超过了隐波，此时卖方大幅亏损，而这就是风险补偿存在的原因。
下图是SPY（标普500ETF）的真实波动与隐波走势图，其中蓝线是真实波动，绿线是隐波。
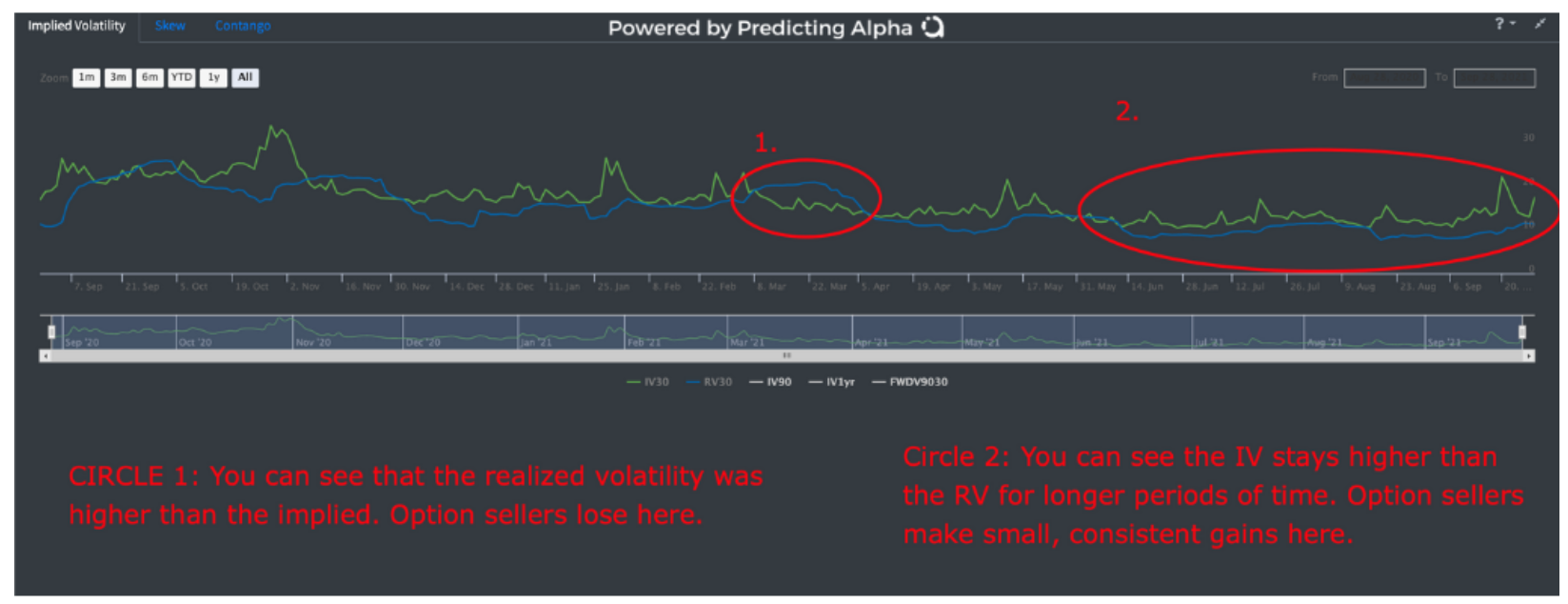
你可以看到点1出真实波动上穿了隐波，此时卖方亏损，点2处，真实波动则一直在隐波下方，卖方慢慢积累盈利。
我们所有人最关心的问题，卖方通过获得风险补偿可以挣多少钱？
长期来看，11%每年。
我想挣的更多，你想挣的更多，11%太拉跨，那我们怎么办？
第六节：买便宜东西，卖贵的东西
让我们再回到房屋的例子，假设我们正在给纽约一个房子估价。突然之间，市场上需求暴增，可供出租的房子急剧减少，租金不断上涨，你看了看你手上的房子，2间卧室，风景不错，正常的租金大概是4000美元/月，但市场上有人出6000美元租你的房子。在这个例子中，你以6000美元出租你的房子，那么你得到了比正常市场状态下更高的租金。
在期权世界中，我们也可以主动寻找在gamma风险一致的情况下，theta更高的合约。想想那些被社交媒体炒作的股票期权，非常多的买家，很少的卖家（谁想承担风险呢？）。
但这也许是很好的机会，如果我们可以给gamma一个合理定价，我们就可以找到具有theta溢价的合约。
这里有一个简单的公式：如果隐波大于你预计的实际波动，卖出！
说的再简单一些：如果期权比股票的波动更贵，卖出！
最难的事情在于你如何利用实际波动给期权定价，这个在后面的章节会阐述。
第七节：一个结合实际波动给期权定价的例子
如果我们用隐波除以实际波动，我们就可以看出隐波与实际波动的差距。
例子：如果隐波/实波 = 1.5，那么期权的价格就比股票的价格贵了1.5倍（简化理解）
我们把历史隐波与实际波动放在一张图对比，我们就可以知道通常两者的差值是多少，也可以看到gamma风险来临时，两者的差值是多少。
本章结语
Theta不是免费的午餐，它是期权的属性之一。理解theta是很重要的事，但更重要的是我们如何给风险定价，这才是成功的交易者长期盈利的关键。
-------------------------------------------其他章节-----------------------------------------------
第二章：一个交易实例
https://www.jisilu.cn/question/445039第三章：寻找具有正期望的交易策略
https://www.jisilu.cn/question/445160第四章：找到你的优势并且打造你的交易系统
https://www.jisilu.cn/question/445359第五章：带你深入理解波动
https://www.jisilu.cn/question/445473第六章：期权散户的十条金科玉律
https://www.jisilu.cn/question/445572第七章：如何交易日历价差
https://www.jisilu.cn/question/445658第八章：如何利用升波赚钱
待施工第九章：学习偏度（Skew）交易
https://www.jisilu.cn/question/445726第十章：只卖高隐波期权？
待施工第十一章：如何在低波环境下交易
待施工第十二章：如何将隐波水平变现
https://www.jisilu.cn/question/445982第十三章：如何进行Delta对冲
待施工
DrChase - 可以少赚，但求不赔。
赞同来自: steven1521 、newsu 、tangle007 、callput 、IMWWD 、 、 、 、 、 、 、 、 、更多 »
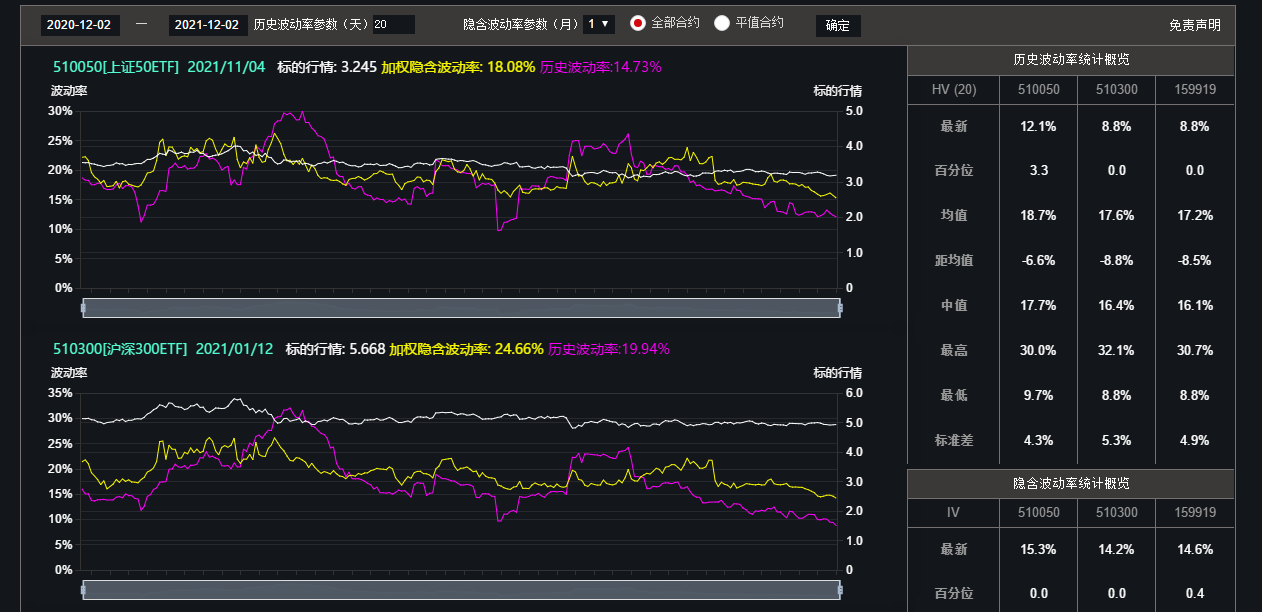
这个期权卖方终极指南系列中很多分析方法都可以通过这个网站实现，与各位分享。
注意，这个网站今年4月后就没有更新了，只能拿来分析历史数据。
DrChase - 可以少赚，但求不赔。
第九章链接：https://www.jisilu.cn/question/445726
对于偏度Skew不熟悉的朋友，建议仔细阅读，我通过本文的翻译对Skew的理解加深了不少。
DrChase - 可以少赚，但求不赔。
赞同来自: neptunus 、bigbear2046 、Tmuer 、人来人往777
关于日历价差的详细讲解目前国内不多见，希望这篇文章能给各位看官一些启发。
链接：https://www.jisilu.cn/question/445658
DrChase - 可以少赚，但求不赔。
赞同来自: Tmuer 、搬砖背锅 、坚持存款 、鱼的世界 、whinbunlee更多 »
强烈推荐认为第一章写的莫名其妙，或者看不懂的人去仔细阅读第四章，很多疑惑迎刃而解。
链接：https://www.jisilu.cn/question/445359
赞同来自: zyynull 、diamondking 、总是人生Guang 、hshpangpang 、灭火勿入 、 、更多 »
这是通达信软件上的。我开户中信证券，这个界面被命名为中信波动率。
京公网安备 11010802031449号