凯利公式:F=p / rL - q / rW
其中p为盈利概率,q=1-p 为亏损概率。
rW为盈利率,等于净盈利除以投入本金,花1万买股票,1.1万卖出那么rW就是0.1而不能是1.1,封基例子里投入1块赚2块,rW就是2,而如果以他的”赌场计算“应该是叫做”1赔3“,这里他其实理解错了。
rL为亏损率,等于净亏损除以投入本金,花一万买股票卖9千,rL就是0.1而不能是0.9,赌场投注一块输光了rL就是1,不能是0。
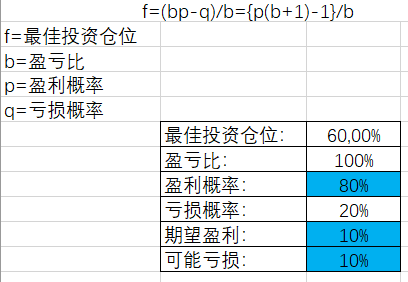
那么我一开始举的例子80%概率盈利10%,20%概率亏损10,那么F=80%/0.1 - 20%/0.1 = 6,算出来6确实会让很多人意外,其实后面 @chineseumi @MoneyBall 等几位网友也解释了,大于1是可以的,表示加杠杆。
具体计算实例见下图
本来excel都拉出来了,事实很清楚,这也能......
------------------------------------------------------------------------------
4/10更新完整解释:
看了一下这个楼里面的回复,很多人显然也是直觉上对于凯利公式可以得出上杠杆的结果表示不相信。但是凯利公式肯定是没错的,可以上杠杆也是没错的,问题出在哪里呢?
问题实际出在,凯利公式的两个表示形式:
通用形式:
F = p / rL - q / rW
其中p为盈利概率,q=1-p 为亏损概率。
rW为盈利率,等于净盈利除以投入本金,rL为亏损率,等于净亏损除以投入本金。
简化形式:
F = (b * p - 1) / (b - 1)
其中p的含义同上,b为”赔率“,定义为在赌博的模式下,每次亏损额为全部投入的赌资,此时的盈利比亏损。
所以,简化版的适用条件为:亏损就会损失全部投入本金。
简化版的F确实是不可能大于1的,因为任何一次亏损都会输光。
但是通用版里面的F是完全可以大于1的。
持有封基写的凯利公式是通用形式,但是他对rW和rL的理解似乎是出了一点问题,在他自己举的例子里面他用的是正确的理解,但是我给出了10%的盈亏率之后,他似乎就搞错了。
本来这个问题纯粹是数学问题,对错非常清晰,我全程没有一句恶语,都是就事论事讨论问题本身,他拉黑不说,还杠精杠精的,真是遗憾。
最后感谢 @zzt2017 @阳光幽灵 @船票96 @MoneyBall 等几位网友的解释。
赞同来自: 好奇心135
import random
class KellyStock:
def __init__(self, g, rW, rL, b): # g-胜率, rW赢时收益比例(净收益比例), rL输时损失比例(净损失比例), b-下注比例
self.__net_worth = 1 # 初始化净值为1
self.__g = g # 胜率
self.__rW = rW # 赢时收益比例,不含本金,例如: 1股1元,买入100股,共花费100元,上涨10%时止盈,则得10元, 则:净收益 = 10% = 0.1
self.__rL = rL # 输时损失比例,不含本金,例如: 1股1元,买入100股,共花费100元,下跌5%时止损,则亏5元, 则:净损失 = 5% = 0.05
self.__b = b # 下注比例
self.__play_times = 0 # 玩的局数
self.__win_times = 0 # 胜利的局数
self.__lose_times = 0 # 失败的局数
def play_once(self):
r = random.random() # 生成一个0到1之间的随机数
if r > 1 - self.__g: # 如果随机数大于胜率(说明: 假如胜率等于0.9, 则1-0.9=0.1 , 代表'百分百的随机数'大于0.1的概率为0.9),表示胜利
self.__net_worth = self.__net_worth + self.__net_worth * self.__b * self.__rW # 胜利,净值增加
result = '胜'
self.__win_times += 1
else: # 如果随机数小于等于胜率,表示失败
self.__net_worth = self.__net_worth - self.__net_worth * self.__b * self.__rL # 失败,净值减少
result = '败'
self.__lose_times += 1
self.__play_times += 1
# print('第', self.__play_times, '局,', result, ',净值:', self.__net_worth)
def play(self, j): # j-局数
for x in range(j):
self.play_once()
# print('一共玩了', j, '局,胜', self.__win_times, '局,败', self.__lose_times, '局,净值:', self.__net_worth)
return self.__net_worth
def play_kelly_stock(g, rW, rL, b, j, n): # 胜率为g、净收益为rW、净损失为rL的局,下注比例为b,每次玩j局,玩n次
total_net_worth = 0
for x in range(n):
k = KellyStock(g, rW, rL, b) # 创建一个KellyStock对象
total_net_worth += k.play(j) # 模拟玩j局游戏并获取总的净值
average_net_worth = total_net_worth / n # 计算平均净值
print('胜率为', g, '、净收益为', rW, '、净损失为', rL, '的局,下注比例为', format(b, '.2f'), ',每次玩', j, '局,玩', n, '次,平均净值为:', format(average_net_worth, '.2f'))
if __name__ == '__main__':
def kelly_股票(p, rW, rL):
"""凯利公式股票版
p (float): 获胜概率
rW - 获胜后的收益(净收益)
rL - 失败后的损失(净损失)
公式为:
f = (p*rW - q*rL) / (rL*rW) = [p*rW - (1-p)*rL] / [rL*rW] = p/rL - q/rW
"""
q = 1 - p
'''这3个是错误的公式'''
f1 = (p*(rW/rL) - q) / (rW/rL)
f2 = p - q*(rL/rW)
f3 = p - (1-p) * (rL/rW)
'''这2个是正确的公式'''
f4 = (p*rW - q*rL) / (rL*rW)
f5 = p/rL - q/rW
# return f1, f2, f3, f4, f5
return f5
胜率 = 0.4
净收益 = 0.1
净损失 = 0.05
# b = [x*0.1 for x in range(1, 101)] # 创建一个下注比例列表
b = [int(x*0.1*1000)/1000 for x in range(1, 101)] # 创建一个下注比例列表
print(f'测试:胜率{胜率},净收益{净收益},净损失{净损失},代入凯利公式股票版后最佳下注比例为{kelly_股票(胜率, 净收益, 净损失)}, 对0-100%之间的各种下注比例,模拟如下:')
for bx in b:
play_kelly_stock(胜率, 净收益, 净损失, bx, 5000, 100)以上代码由于计算机浮点数计算精度问题,公式p/rL - q/rW计算的结果与python跑出来的结果有一定误差,但你可以看到赚钱的趋势是在计算出来的仓位值左右徘徊,另外,有没有大佬可以改进一下这个精度问题,关于这段代码也可以去知乎搜 “凯利公式股票版的python验证”大家一起探讨
集思录的代码排版有问题,特此说明一下如何排版:play_once()、play() 属于类KellyStock的方法,play_kelly_stock()是个单函数,if __name__ == '__main__':下面的所有代码缩进4个空格即可
但是股市不和赌局一样,很难有一把清关,而且有止盈止损机会,股市适合采用凯利公式的通用模式。你上的资金6倍杠杆,分成10个,20个,50个仓位。实际每个仓位分配到的资金比例是60%/10=6%,60%/20=3%,60%/50=1.2%。t通过多仓位的大数定律(赢利概率和赔率)来获得正期望收益。
请教一个问题,根据凯利公式算出来投资比例,是总资金的比例还是剩余现金的比例。因为股票不像赌博秒开,可能有持仓情况,比如我现在5成仓位,算出来F=30%,那么下一次是投入3成仓位,还是1.5成仓位呢?一般来说是总资金比例,股票来说你认为是可用资金比例当然也没有什么问题
谢谢楼主,凯利公式中如果胜率50%,输赢的赔率50%,那么F应该等于0,因为期望值收益为零,当p等于1时,这个凯利公式就只跟输的赔率有关,而且要加杠杠是吗?p等于1意味着100%的概率赚钱,如果真有这样的事情,当然是你能加多大杠杆就加多大杠杆。不过如果不是100%,哪怕99.99%,如果失败会赔光,凯利公式也不会允许你加杠杆。如果失败损失不会赔光,那么根据凯利公式,是可以计算出加杠杆的结果的。比如前面有人提到的期权其实就是一个很好的例子。
实际情况杠杆也有成本,比如存银行是一件100%赚钱的事,但是谁能借到比存款利率还低的贷款呢...如果马云肯不要利息借钱给我,那我肯定要借上100亿啊...
为什么会有0.1%概率亏完呢?就是做数学计算,算了就明白了
凯利公式只是保证了数学上给出收益率最大化的仓位,至于你输入的参数如果与现实不符,那不是凯利公式的问题。
你如果觉得我计算有问题可以直接说出来。
这样算的问题是,实际情况可能是为什么会有0.1%概率亏完呢?
80%概率 挣 10%,19.9%概率亏 10%, 0.1% 概率亏完。
再算算仓位!
凯利公式只是保证了数学上给出收益率最大化的仓位,至于你输入的参数如果与现实不符,那不是凯利公式的问题。
你如果觉得我计算有问题可以直接说出来。
赞同来自: zengyongqiang
关于人为设置止损,是不能提高仓位加杠杆的。人为设置止损是可以的。
极端点,1%就止损,会发现理论仓位大了很多。
现实的情况很容易是,大部分时间都在不停的止损。
至于你说的不停的止损的问题,你引用的@阳光幽灵 的回复里面其实已经说明了,改变止损点的同时,也会改变胜率的。
比如当前点位买入沪深300,如果你止损设到50%,恐怕胜率接近100%,但是止损设1%,胜率就要接近0%了。
凯利公式是纯数学上保证了,如果你输入的胜率和盈利/亏损都是正确的,那么它输出的仓位比例就可以获得最大的期望收益率。至于胜率本身估计错了,或者止损点不可行,那就是另外的问题了。
赞同来自: mumu33
这和分级B非常类似。
比如5倍杠杆的话。
跌10%,杠杆由5倍变为10倍。
涨10%,杠杆由5倍变为3.33倍。
为了保持杠杆不变,就会导致涨被迫加杠杆,跌被迫缩杠杆。
涨跌幅度变动越大,杠杆升缩现象越严重。
每一次波动都会导致资产缩水。
如果不加满仓,保持恒定仓位比例,就转变为跌时加仓,涨时减仓。
能加多少杠杆取决于波动率,而不是收益率。
比如债券波动率小,可以允许杠杆率,就高于股票。
账户已注销 - 过去发生的频率不代表未来发生的概率。
但单次赌注不归零,自然是可以加杠杆的。
感谢下帖主,我今天有东西写了。
看了一下回帖,发觉不少人对资金管理都没有入门,有可能对交易系统的R乘数分布也缺乏概念。没错,在破产风险下,凯利公式弱爆了
有人把单次交易投入本金与单次交易风险金混淆了,应用凯利公式才会就会得出大于100%的杠杆投入这样的荒谬结论。
胜率和赔率反应出的期望值对一个交易系统来说固然重要,但是,交易单子的时间序列分布隐藏的恐怖杀伤力通常被大大低估。任何交易系统无论采用多么小的风险管理和资金管理方法,都存在最终破产可能性。历史最大回撤对于...
一、通用版本的凯利公式适合于投资领域这个回复大概是本楼里面最详细全面的,多谢了。
我们日常经常接触到的凯利公式,指的是下面这种简明版的凯利公式:
f* =(bp-q)/ b
在公式中,各参数意义为:
f* = 应投注的资本比值
p = 获胜的概率
q = 失败的概率,即1 - p
b = 赔率,等于期望盈利 ÷可能亏损(也就是盈亏比)
公式上面的分子bp-q代表“赢面”,数学中叫“期望值”。
什么才是不多不少的合适赌注呢?凯利告诉我们要通过...
问题实际出在,凯利公式的两个表示形式:
通用形式:
F = p / rL - q / rW
其中p为盈利概率,q=1-p 为亏损概率。
rW为盈利率,等于净盈利除以投入本金,rL为亏损率,等于净亏损除以投入本金。
简化形式:
F = (b * p - 1) / (b - 1)
其中p的含义同上,b为”赔率“,定义为在赌博的模式下,每次亏损额为全部投入的赌资,此时的盈利比亏损。
所以,简化版的适用条件为:亏损就会损失全部投入本金。
简化版的F确实是不可能大于1的,因为任何一次亏损都会输光。
但是通用版里面的F是完全可以大于1的。
持有封基写的凯利公式是通用形式,但是他对rW和rL的理解似乎是出了一点问题,在他自己举的例子里面他用的是正确的理解,但是我给出了10%的盈亏率之后,他似乎就搞错了。
本来这个问题纯粹是数学问题,对错非常清晰,我全程没有一句恶语,都是就事论事讨论问题本身,他拉黑不说,还杠精杠精的,真是遗憾。还有一堆跟风的,希望你们回去拿个excel算算......
最后感谢 @zzt2017 @阳光幽灵 @船票96 @MoneyBall 等几位网友的解释。
假设使用5倍杠杆,亏损扩大为50%,净资产缩水50%,这时杠杆实际就升为10倍杠杆,如果保持筹码不变,只能变现部分筹码。
如果又上涨10%。
假设使用5倍杠杆,净资产只能恢复原来75%。
如果下跌10%
假设使用50%仓位,亏损为5%,净资产缩水5%,这时因筹码价格变低,如果要保持筹码在总资产比例,还需要增加筹码5%。
如果又上涨10%。
假设使用50%仓位,这时净资产是增加的。增加资产为0.05*0.1=0.005。
这时我们会发现杠杆不变情形下,被迫在低位减筹码,在高位加筹码,每一次波动都会有损失。
如果没有仓位加满的话,仓位比例不变情形下,就会在低位加筹码,在高位减筹码。
这实际就是一个网格策略。
赞同来自: zengyongqiang 、xineric 、超弦资本 、linuxjava01 、xf1973更多 »
容我笑一会……
首先凯利公式应对的是赌场下注,非投资场景。即使胜率100%,凯利公式结果也只是下注所有资金(当然100%胜率加杠杆不必讨论)。
举个反例,按照楼主本金10000,6倍杠杆下注,连输3把(这个概率大数法则下不难出来吧)本金640已经亏了90%以上啦!对应投资是不是灭顶之灾?
凯利公式只能辅助投资而已,连后期使用凯利公式的索普(最早使用凯利公式应用于股票投资),都是算出凯利公式下注筹码减半辅助自己的投资。
能否使用杠杆关键在于控制回退的能力,而不是在于收益率有多高。
用收益率决定杠杆率是错误的。
只有收益预期是正收益,最大回退在可控制范围内,使用杠杆才是安全。
否则蹦盘是早晚的事。
人一定要有底限思维,不要去触碰底限,一旦过了底限,就无法收拾残局。
通常情形下,债券出现回退要小于股票,债券预期收益率未必很高,但可以使用更高杠杆,通常可以大于股票。
有人把单次交易投入本金与单次交易风险金混淆了,应用凯利公式才会就会得出大于100%的杠杆投入这样的荒谬结论。
胜率和赔率反应出的期望值对一个交易系统来说固然重要,但是,交易单子的时间序列分布隐藏的恐怖杀伤力通常被大大低估。任何交易系统无论采用多么小的风险管理和资金管理方法,都存在最终破产可能性。历史最大回撤对于交易实践具有更大的实用价值。
凯利公式对于资金管理而言只适合作为一个入门概念,严肃的交易者应该继续探索像固定分数法,固定比例法,变动比例法等更为稳定的资金管理方法,并以这类方法基础,才有在市场上最终幸存并获利的可能。
实际你是通过止损,来限制亏损额度,提高盈亏比。
投资博弈不只是盈亏概率,实际还博弈盈亏比。
实际在能保证赢利前提下,增强博弈次数,也可以增强收益。
对于回退幅度大的投资者需要降低仓位,反之可以加大仓位。
如果回退控制不好,贸然加大仓位就非常危险。
赞同来自: adamen 、無空 、namesou 、syyep 、suprep 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、更多 »
我们日常经常接触到的凯利公式,指的是下面这种简明版的凯利公式:
f* =(bp-q)/ b
在公式中,各参数意义为:
f* = 应投注的资本比值
p = 获胜的概率
q = 失败的概率,即1 - p
b = 赔率,等于期望盈利 ÷可能亏损(也就是盈亏比)
公式上面的分子bp-q代表“赢面”,数学中叫“期望值”。
什么才是不多不少的合适赌注呢?凯利告诉我们要通过选择最佳投注比例,才能长期获得最高盈利。回到前面提到的例子中,硬币抛出正反面的概率都是50%,所以p、q获胜失败的概率都为0.5,而赔率=期望盈利÷可能亏损=2元盈利÷1元亏损,赔率就是2,我们要求的答案是f,也就是(bp - q) ÷ b = (2 * 50% - 50%) ÷ 2 = 25%。
拿出资金的25%来进行下注,才能使赌局收益最大化。
遗憾的是,平常人并不去赌场,也没有机会将这个公式应用于赌博场景中。
但是,各路大神将它应用于类似于“赌博”的场景——股市中,这就有可能犯一些“适用范围”方面的错误。
在上面的例子中,每一次下注都只有两种结果:“输光全部本金”或者“赚一些钱”。
但是,股市并不是这样运作的,因为,每一个把股市视作赌场的赌徒,都会有一些止损的方法,比如说,输掉10%之后我就割肉走人了。而且单只股票直接退市价值毁灭的概率也是很低的。这就导致了“输光全部本金”这种结果在股市中出现的概率很低几乎不可能,简单凯利公式在这里其实是不适用的。
f =(bp-q)/ b=p-q/b=(1/b+1)*p-1/b
而p是一个大于等于零,小于等于一的数,那么当且仅当p=100%的时候,f=100%。
也就是说,我们100%赚钱了,我们才能满仓。也就是说,我们把钱全部存在银行定期里面就好了。但是常识告诉我们,如果一个投资机会能100%赚钱,那么我们应该借钱去投资,把杠杆加满(前提是收益要覆盖掉杠杆成本)。那些满仓轮动不择时的投资者难道都是错的?
还是那句话,问题出在了我们炒股不可能全部赔光,这就使得简明版凯利公式太保守了。
正确的做法是使用通用凯利公式:
f=p/rl-q/rw
在公式中,各参数意义为:
f = 应投注的资本比值,即你的股票仓位
p = 获胜的概率
q = 失败的概率,即1 - p
rw = rwin,当你赌对了,你的盈利的比率(不包含本金)
rl=rloss,当你赌错了,你的亏损比率
也就是说,简明凯利公式里面的b=rw/rl
当rl=100%时,通用凯利公式就变成了简明凯利公式。
也就是说,对于股票市场,如果你设置了一定的止损位,保证在每一次下注的时候不会亏光全部本金,那么这个时候你再用简明凯利公式来计算仓位就太保守了。
我们用简明凯利公式用得很习惯的原因是“过度自信”,我们会把有5%概率发生的事情“自我包装和强化”成有50%概率发生,我们总是受到近因效应影响,困在自己的信息茧房里,并且把接收到的信息都当做是提高自己获胜概率的证据。这样的话,简明凯利公式的“保守”和我们过度自信的“冒进”就相互抵消掉了一部分,导致我们的整体仓位不轻也不重。
这就产生了一个提醒:如果你用通用凯利公式,那么你就不能犯“过度自信”的错误!
二、通用凯利公式中的胜率与赔率
在通用凯利公式f=p/rl-q/rw中,胜率和赔率好像非常对称,那么,在公式里面,胜率和赔率是同等重要的吗?
我换一个问法:如果一个投资标的是有很大概率获得中等的收益,另一个投资标的是有中等的概率获得很大的收益,那么你应该投哪个呢?
我们来模拟一下:
标的一:胜率25%,正确时候的收益率33.33%,10%止损(错误时候的损失率),那么:
f=25%/10%-75%/33.33%=25%
标的二:胜率33.33%,正确时候的收益率25%,10%止损(错误时候的损失率),那么:
f=33.33%/10%-66.67%/25%=66%
问题来了,为什么胜率和收益率互换了一下位置,仓位就会翻倍?难道说,凯利公式真的重胜率,轻赔率吗?
我们先来看一下标的一的期望值:
标的一的期望值=25%*33.33%-75%*10%=0.008325
标的二的期望值=33.33%*25%-66.67%*10%=0.016655
也就是说,当期望值翻倍的时候,仓位也基本上翻倍了。
两个标的进行四次投资,收益率均不含本金
正确次数
25%胜率,33%收益
33%胜率,25%收益
收益率
概率
预期收益
收益率
概率
预期收益
0
0.9^4-1
0.75^4
收益率*概率
0.9^4-1
0.67^4
收益率*概率
1
0.9^3*1.33-1
4*0.25*0.75^3
收益率*概率
1.25*0.9^3-1
4*0.33*0.67^3
收益率*概率
2
1.33^2*0.9^2-1
6*0.25^2*0.75^2
收益率*概率
1.25^2*0.9^2-1
6*0.33^2*0.67^2
收益率*概率
3
1.33^3*0.9-1
4*0.25^3*0.75
收益率*概率
1.25^3*0.9-1
4*0.33^3*0.67
收益率*概率
4
1.33^4-1
0.25^4
收益率*概率
1.25^4-1
0.33^4
收益率*概率
合计
计算结果如下:
左边的标的,能够产生更大的收益,但是概率值很低,它更像是那种“彩票型”股票,是低胜率高赔率的投资标的,属于短线玩一票大的。
右面的标的,相当于长期投资,属于“稳稳的幸福”,概率高,赔率中等。
不管怎么算,标的二的期望值,都基本上是标的一的2倍,所以,标的二更值得加重仓位。
如果市场是有效的,胜率和赔率一般是反比例变动,不给任何人套利的机会。但我们炒股就是要寻找这种胜率和赔率出现不对称的情况。
如果你想一直在市场中存活下去,高概率总是优于高赔率的,也就是说,尽量少碰“彩票型股票”,因为彩票型股票更容易让你犯错,让你控制不住自己的情绪。我们要追求的是“高概率”,等待“击球区”,等待出手的时机,如果时机不好,就坚决不出手。这很像孙子兵法中说的“先为不可胜,以待敌之可胜,不可胜在己,可胜在敌”:
先为不可胜:首先要保证自己是不可被战胜的,保住你的本金,长久地在市场中存活下去。
以待敌之可胜:静静地等待出手的时机,像是隐藏在阴暗角落的狙击手,出手就有很大的概率击杀。
不可胜在己:不可被战胜是自己能够控制的,你要控制好自己的情绪,控制你的心态不要崩溃,从而不可被战胜。
可胜在敌:能否取得胜利,能否实现盈利是自己控制不了的,而是全靠“等”,等待对手盘情绪崩溃,当然,如果等不来,你就只能继续等,因为这是外部客观环境,你控制不了。
三、通用凯利公式与止损
重新审视一下凯利公式表达式f=p/rl-q/rw,似乎当止损线rl越小的时候,我们越应该加重仓位才对?其实不是的,这里面存在着一个变动关系:
当rw一定的时候,p与rl存在正相关关系,rl越大,p越大。
这似乎很好理解,你能承受的最大回撤越大,那么未来股票上攻收复失地的概率就越大,你就越能等到回本的那一天,如果你每次都是1%就止损,那么这支股票稍有无效波动你就止损,你就一直不停的在止损或者在止损的路上。
经过测算,会有两个结论:
1、rl=8%~10%的时候进行止损,f的值会趋向于最大状态。
2、rw越大,止损比例应该越小,也就是说,这只股票长得越像是“彩票型股票”,你越应该设置一个小的止损比例。因为道理很简单,彩票型的股票会让你更多地犯错,市场上不可能有那么多只彩票型股票,事实上他们非常罕见,你犯错的概率大大增加了。你如果止损比例很大,有可能会快速地输光。只有止损比例调小了,你的“容错率”才会增大,你才能更有可能在市场中长期生存下去。如果你对一般的单只股票30%~50%进行止盈,止损线设定在10%,那么你在购买“彩票型股票”比如翻倍股的时候就应该将止损线设定在6%~7%左右,割得早才能活得久。
四、通用凯利公式与杠杆
如果一个标的,胜率为33.33%,收益率为30%,10%止损,那么按照凯利公式:
f=p/rl-q/rw=33.33%/10%-66.67%/30%=1.11066666667
也就是说,操作这个标的,胜率是33%即可满仓,我们甚至可以加一个1.11x的杠杆。
为什么?简明凯利公式因为有损失全部本金的风险,所以,你永远都不能ALL IN,并且永远都不能加杠杆。这在简明凯利公式的表达式可以直接用肉眼看出来:
f* =(bp-q)/ b=p-q/b
p是一个大于等于零,小于等于一的数字,q/b也是一个大于等于零,小于等于一的数字,二者相减,结果肯定小于一,且如果相减为负数,说明你的期望值为负,你应该跑到你的对手盘的阵营中去(做多改做空,做空改做多)。
但是股票市场由于有止损线这个限制,你不可能损失掉全部本金,赌局的安全系数,投资者的生存概率大大提高了,我们就可以去杠杆操作。
船票96
 - 控制回撤第一要务
- 控制回撤第一要务
还上杠杠??举列中单次投注要么是盈利10%,要么亏损10%,是不存在单次亏光本金的可能。
只要有亏光资金的概率(1-b)存在,则不管盈利有多大,都不要投入比例超过P的资金。
比例=(胜率*赔率-1)/(赔率-1)
当胜率是是100%,赔率是无穷大,比例的极限也只能是1啊
自己用高数在推导一次
当然在实际中是不存在这么理想化的条件存在。
比如左轮手枪有5个空弹,只有1颗子弹。
如果进行轮盘赌。
只发射1颗子弹和连续发射5颗子弹,它们发生致命性概率相同吗?
任何带有致命风险游戏,必须克制性参与游戏。
游戏不只是考虑胜率,还要考虑盈亏比。
这里只是假设只是亏10%,放大6倍杠杆极限损失60%,还有40%可以需命,还能玩下去。
实际一次回退60%。
如果仓位为60%的话,实际一次回退6%。
回退过大,并非利于财富增长。
回退一次累计性,增长需要多次连续增长。
控制仓位目的是控制回退幅度。
赞同来自: kingsun2000 、老胜 、zhenglonggeng 、眼睛 、moonlighting 、更多 »
楼主是对的。
-以下引用封基老师的帖子----------------------------------------------------------------------------
凯利公式明确的指出了下注的比例有个最佳值,超过或者小于这个最佳值的收益率都不是最高的。我们通过一个实际的例子会更加看的清楚:
假定有个赌局,盈利概率80%,盈利金额为2元。亏损概率为20%,亏损额为1元(本金亏光)那么按照凯利公式,应该每次下多少赌注呢:
F= p/r1-q/rw=80%/100%-20%/200%=80%-10%=70%。
封基老师也是一样的算法,有问题吗?只要有亏光资金的概率(1-b)存在,则不管盈利有多大,都不要投入比例超过P的资金。
比例=(胜率*赔率-1)/(赔率-1)
当胜率是是100%,赔率是无穷大,比例的极限也只能是1啊
自己用高数在推导一次
赞同来自: 泰瑞柏年 、xf1973 、mikelazyman 、Sybil廖
仓位控制取决于盈亏概率和盈亏比而定,与具体盈亏率无关。
F=0.6,而不是F=6。
如果F大于1的话,可能任何一次错误,就可以清零。
如果控制仓位为60%的话,本金长期增长最佳仓位。
这只是纯学术探讨。
dhhlys - 积重而返
赞同来自: abcdefgh123
1.只要亏损不存在一波亏完,赢的时候如果足够多的话就有可能加杠杆。
2. 如果ic现在贴水是年华50%,然后你有120万,必然多两手优于一手。
3. 加杠杆的凯利公式本质上就是 @账户已注销 大佬的加杠杆动态平衡,我反正已经实践了。
赞同来自: abcdefgh123
魔铁潜水艇 - 看你们赚钱比我自己亏还难受
赞同来自: skyblue777 、wuchunlong 、bismackzhang 、Sybil廖
而且还涉及一个兑现时间问题,选项A三个月就可能涨50%但也可能跌,选项B稳涨50%但可能需要三年时间。这种时候就很难取舍……
赞同来自: abcdefgh123
(0.8*0.1-0.2*0.1)/0.01=6
真实的是什么呢
0.8-0.2=0.6,也就是最大60%仓位,盈亏比可以互除
赞同来自: 庸人字扰之 、suprep 、hjndhr 、好奇心135 、moonlighting 、 、 、 、 、 、 、更多 »
1)假设N次投资,如果N足够,赢的次数为Np,亏的次数为Nq=N(1-p)
2)假设每次投入总资金比例为x,假设总资产为1,假设rW和rL的定义如楼主所说。
3)如果某次投资赢,则资产变为 (1-x)+x(1+rW)=1+x*rW;如果某次投资输,则资产变为(1-x)+x(1-rL)=1-x*rL
由1)可知,N次投资,胜利次数为Np,失败次数为N(1-p),最初资产为1,则结合3)进行N次投资后总资产变为:
W=(1+x*rW)^Np*(1-x*rL)^N(1-p),等式取对数得到:
logW=Nplog(1+x*rW)+N(1-p)log(1-x*rL)
如果要让logW最大,对等式求导使其为0
Np*rW/(1+x*rW)-N(1-p)*rL/(1-x*rL)=0
得到: rW*rL*x=p*rW-q*rL
即x=p/rL-q/rW时投资收益增长最快。
80%概率盈利10%,20%概率亏损10,那么F=80%/0.1 - 20%/0.1 = 6,就是可以加5倍杠杆。
不过投资最大的问题在于你很难对胜率和赔率进行预测,对于股票胜率和赔率均无法预测,对于固收类产品赔率可能可以得到,但胜率很难提前预测,所以实际投资要精确套用凯利公式会比较难。
 Edge
Edge Chrome
Chrome Firefox
Firefox

 京公网安备 11010802031449号
京公网安备 11010802031449号