Edge
Chrome
Firefox
今天无意翻到可转债平均收益率数据，联想到曾经的“国债收益率—股票PE中位数倒数”估值方法，尝试套用给可转债市场估值。
一、思路
十年期国债收益率一般被定义为市场无风险收益率的基准。
而资本又存在从低收益市场流向高收益市场的天然行为属性，理想模型下，当十年期国债收益率升高时，国债会吸纳资本，造成其他市场资金流出造成下跌，反之亦然。
所以，试用十年期国债收益率与可转债平均收益率，给可转债市场估值。
二、整理数据
数据范围由2018/1/2至2023/5/5最近一个交易日，
从网上分别获取十年期国债收益率和可转债平均收益率，共计1295个数据。
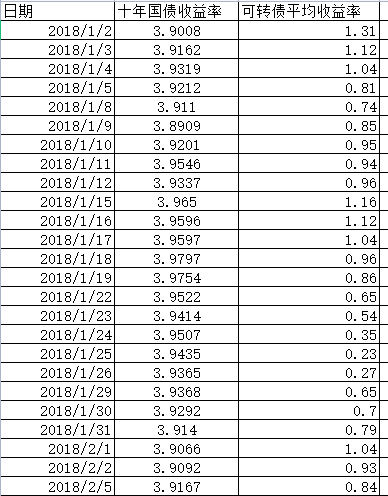
然后用十年期国债收益率减去可转债平均收益率，差值暂且称为风险比率，风险比率越大，说明十年期国债越有吸引力（相对而言可转债越没吸引力），可转债市场越高估。简单绘图。
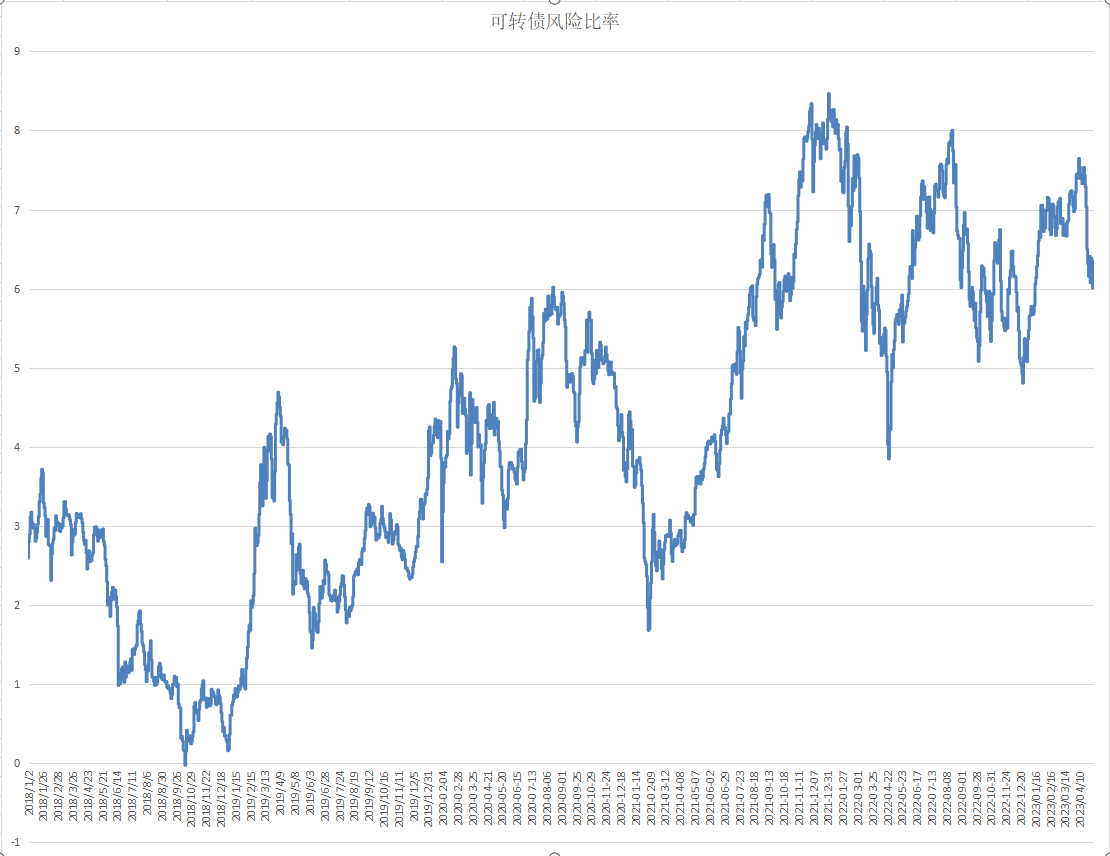
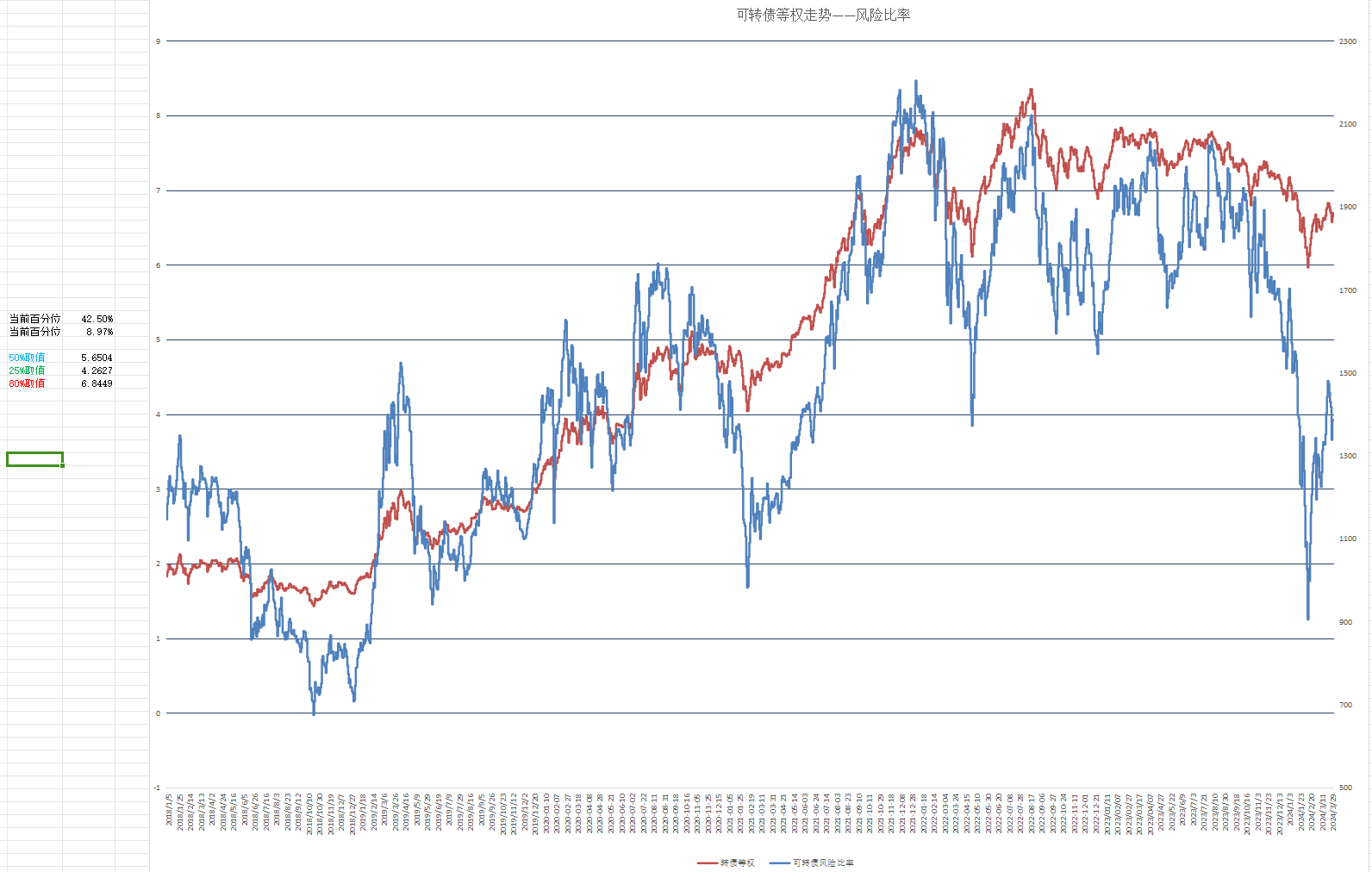
这个图好像看不出什么，我们再叠加可转债等权走势
可以看出风险比率走势与可转债等权走势具有强相关性，试对比其他估值方法，如凌波大神使用的平均双低。
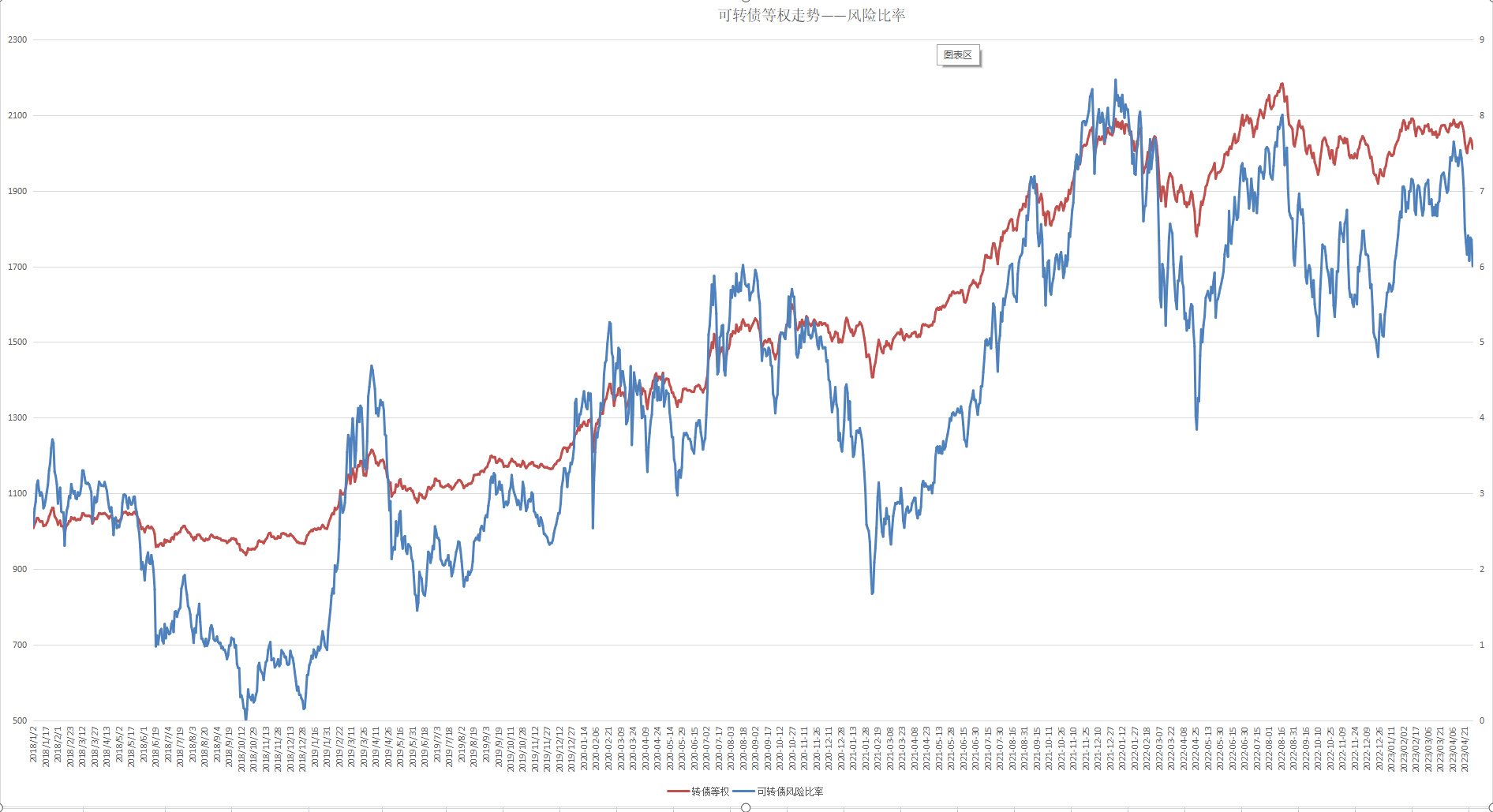
如图中红色的2019年6月10日等权指数1081点（平均双低128.71），和2021年2月8日的1408点（平均双低150.19）的估值是差不多的。
又如紫色的2020年9月28日的等权指数1455点（平均双低147.44），和2022年4月26日的1779点（平均双低188.51）的估值是相当的。
在这些位置后面都出现了一定的涨幅，但用后一个数据的平均双低来说已经高估了，可见简单采用平均双低估值的话可能存在一定的局限性，
从这个角度看，并不是等权指数越大，平均双低越大，估值就越高。
三、数据简单运用
从上图可以看出，风险比率从0至8%之间震荡。
分别提取20、40、50、80百分位的数据，如图
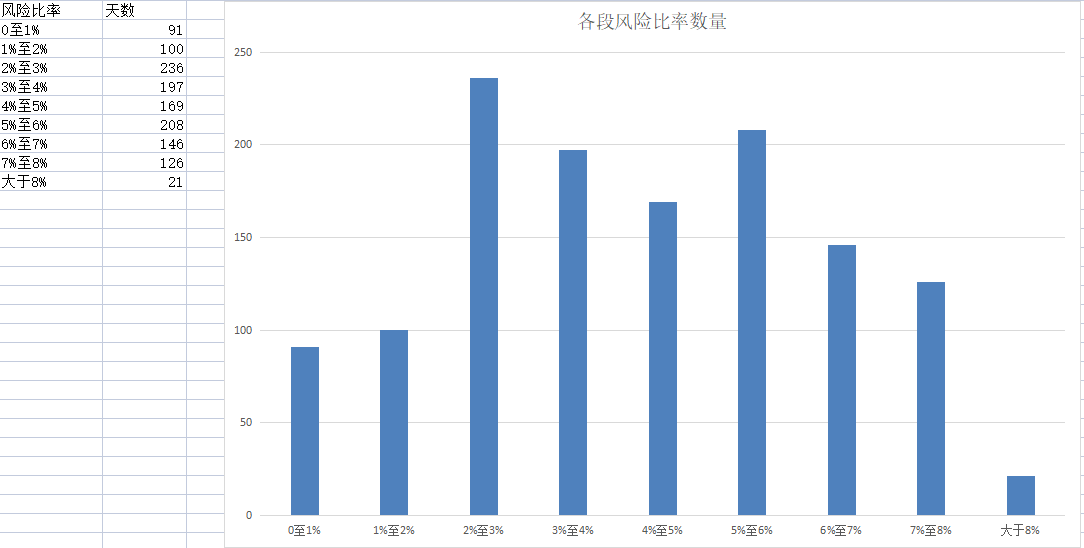
我们再以1%为间断分别统计一下数量。
可以看出，大部分时间都是在2%至8%之间震荡的，这又进一步给我们缩小了实际用到的估值范围。
可以简单运用一下，可否用2%至8%来分段分别控制持有可转债的仓位呢？
我们寻找一个橄榄型的数据模型，极度低估和极度高估的少数，偏低—合理—偏高是常态，
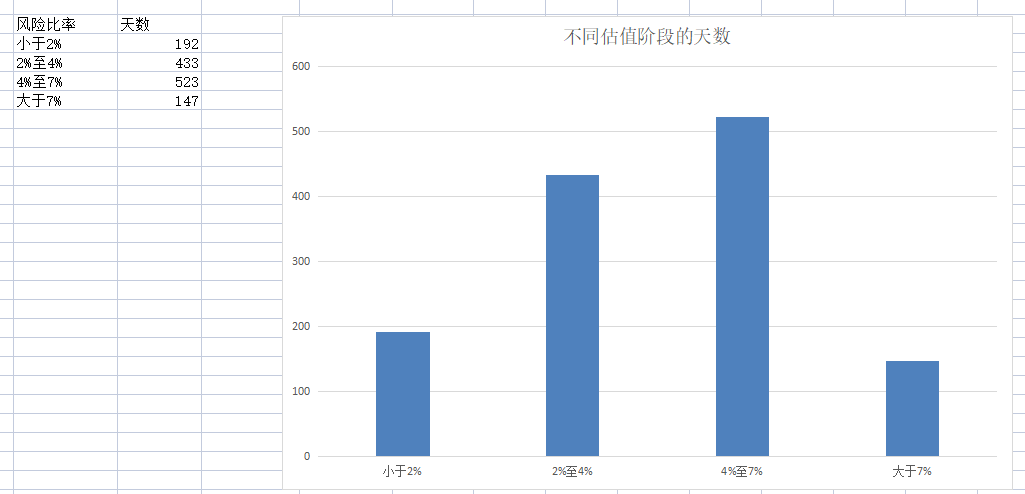
大概分为四段，如图
如，当风险比率大于7%时，可转债市场处于高估阶段，逢高减仓或空仓。
当风险比率4%—7%时，可转债市场处于估值合理阶段，持有大部分仓位。
当风险比率小于在2%至4%时，处于低估状态，适量加仓。
当风险比率小于2%时，处于极度低估状态，满仓。
而当前5月5日风险比率为6.0038%，处于历史以来77%的位置，在中间偏上位置，大家根据自己的风险承受能力能给予多少仓位呢？
四、一些联想
在股票市场，近十年平均PE大约是25倍，倒数1/25即股票市场4%的收益率为合理估值。
而18年至今可转债市场平均收益率为-1.12%，似乎-1.12%是可转债被大众普遍接受的估值，足足比股票市场高出5%，这大概是可转债下有保底、上不封顶的特性给予这5%的溢价吧。
以上是个人的一些思路，欢迎大家一起交流。
赞同来自: laolii 、好奇心135 、gaokui16816888
当前可转债风险比率为3.92，处于2018年至今的42.5%百分位，仍是低估状态。
目前根据历史情况暂定风险比率大于7为高估。
你用时间国债减可转债平均收益的差和可转债等权去求相关，属于典型的自相关问题，或者你可以不用差额，你直接用可转债平均收益的负值去和等权指数去对比，肯定是强相关，因为转债整体上涨必定要降低平均收益，也必定等权指数拉高。其实简单点直接用可转债平均收益率也会得出和你一样的结论，不信你可以尝试把十债去掉。最后，其实平均收益是失真的，不同等级转债的平均收益有巨大不同，大块头一般长的慢，到期收益就显得高，我建...话糙理不糙，这个方法的确和只需要观察转债收益率大致在-4%～+2%效果基本一致。
赞同来自: gaokui16816888
2021 年 2 月份国债收益率接近 4%的时候，国债收益率开始回落，可转债不是下跌，而是开始上涨，一直到到 2022 年初，所以你这个推理看起来不成立。正是国债收益率下滑，导致国债已经没那么大的资金吸引力，资金就会流向相对高的可转债市场，从而拉抬可转债。
用文种的模型来说，国债收益率下滑，导致差值降低→即估值降低，存在抬升空间。
赞同来自: 过眼云烟
假设两个时间可转债收益率都为-1%，十债收益率分别是3%和4%，十债为4%时间的资金流向国债的动力肯定更大，造成可转债回调压力也更大，我作差值是为了体现资金的相对流动动力情况。2021 年 2 月份国债收益率接近 4%的时候，国债收益率开始回落，可转债不是下跌，而是开始上涨，一直到到 2022 年初，所以你这个推理看起来不成立。
这个不现实的。可以想象一下极端情况，如果真的有一种方法能够准确定价，并且通过这种方式套利可以瞬间让市场价格达到算出来的公允价格；那么，这个市场也就死了、就不再波动了，而是一条横线的心电图。这种事情在现实中也是有案例的。比如，壳牌在北海布伦特原油的衍生品市场上曾经几次特别强势，但后来他们都主动修改了一些条款。为什么呢？因为大家都知道只有你能赢，就不玩了；大家都不玩了，市场的主宰也赚不到钱。为了能长...你这个有一种“如果有精确定价，市场就死了”的观点我不认同。股指期货、期权算得上精确定价了吧，也没见哪个国家的股指期货死了。
而且，可转债和正股没法做空，套利没法进行。本身衍生品就是风险中性定价，只要现货在动，衍生品就要动，根本不存在死这一说法。
只是不见得持有偏离理论价格最大的最赚钱倒是了，奇异期权的每个希腊字母（或者说衍生品因子）不见得收敛速度一样。而且因为不能做空正股，裸持有转债还要受股票多因子模型的影响。
赞同来自: XIAOHULI92 、Branes 、topdeck 、七剑下天下 、fuyda 、 、 、 、 、 、 、 、更多 »
等把这些问题解决了，就差不多了。目前国内厦门大学的郑振龙有文章（没有解决脉冲问题，但现在新规后，似乎脉冲没了），可以去参考，其他定价都是残本。这个不现实的。可以想象一下极端情况，如果真的有一种方法能够准确定价，并且通过这种方式套利可以瞬间让市场价格达到算出来的公允价格；那么，这个市场也就死了、就不再波动了，而是一条横线的心电图。
这种事情在现实中也是有案例的。比如，壳牌在北海布伦特原油的衍生品市场上曾经几次特别强势，但后来他们都主动修改了一些条款。为什么呢？因为大家都知道只有你能赢，就不玩了；大家都不玩了，市场的主宰也赚不到钱。为了能长期赚钱，他们愿意有时候输一部分回去。赌场也是这个道理。
市场存在的意义，就是要有分歧，才有参与者，才有流动性、才好长期得玩下去。
上面的估值，就是让我们能够粗略得知道周期的高低；“模糊的正确”对大多数人来说就足够了。
赞同来自: momo235 、fuyda 、青火 、好奇心135 、gaokui16816888更多 »
蒙特卡洛仿真需要解决几个问题：1 波动率。这个波动率是未来波动率，不是过去的。比较粗暴的做法是用过去一段时间的日收益率的标准差来表征，然而这太粗暴了，精度很低，可以去看看kaggle的比赛，专门预测波动率已经是各种深度学习上了。2 强制赎回，赎回条件到了，管理层到底执行不，这是个概率问题，也就变成了分类问题。（特征自己开脑洞）如果执行，下次强赎记数时间的开始又是个回归问题。（依旧特征自己开脑洞）。3 对于不理性脉冲的定价，这个类似于vix期货长期升水，对应到靠转债就是小盘债的溢价率偏高。其实就是对脉冲的定价。
等把这些问题解决了，就差不多了。目前国内厦门大学的郑振龙有文章（没有解决脉冲问题，但现在新规后，似乎脉冲没了），可以去参考，其他定价都是残本。
赞同来自: skyblue777 、大饼炒鸡蛋 、一基当千 、fuyda 、渴了可乐 、 、 、 、 、更多 »
我觉得，你的这个思路挺好的。
我用的Wind的数据源，取得 可转债价格的中位数、可转债纯债到期收益率的中位数、10年期国债收益率。
从估值周期的角度看，周期性更强、也更稳定一些（主要就是上下波动，没有向上的斜率）；具体参见第一张图。同时，也可以对比看一下第二张图，是单纯的纯债到期收益率，感觉就略差一些了。
另外，用中位数还有一个好处。截止到目前为止，中位数价格基本没有超过130元 —— 130元以下，债性会比较强；用纯债到期收益率衡量也相对更合理一些。
换言之，中位数要比平均值更合理一些。
你用时间国债减可转债平均收益的差和可转债等权去求相关，属于典型的自相关问题，或者你可以不用差额，你直接用可转债平均收益的负值去和等权指数去对比，肯定是强相关，因为转债整体上涨必定要降低平均收益，也必定等权指数拉高。其实简单点直接用可转债平均收益率也会得出和你一样的结论，不信你可以尝试把十债去掉。最后，其实平均收益是失真的，不同等级转债的平均收益有巨大不同，大块头一般长的慢，到期收益就显得高，我建...假设两个时间可转债收益率都为-1%，十债收益率分别是3%和4%，十债为4%时间的资金流向国债的动力肯定更大，造成可转债回调压力也更大，我作差值是为了体现资金的相对流动动力情况。
赞同来自: 青火 、Duckruck 、fuyda 、huron 、甘泉 、 、 、 、 、更多 »
其实简单点直接用可转债平均收益率也会得出和你一样的结论，不信你可以尝试把十债去掉。
最后，其实平均收益是失真的，不同等级转债的平均收益有巨大不同，大块头一般长的慢，到期收益就显得高，我建议用收益率中位数来替代。其实结果是一样的，其实无论哪种算法，结论一定是：可转债XX收益高的时候，转债底部，估值相对便宜。所以不客气地说，楼主有点脱裤子放屁，加一个十债收益率其实对结果没有什么优化
京公网安备 11010802031449号