可转债作为小散友好的品种,具有下有保底,上不封底的特点,因此对可转债历史交易数据进行分析,意图获取优秀的可转债交易策略应是小散们追求更高和更平稳收益的一种方式。笔者最近开始接触和学习可转债的量化投资策略,在这里将数据获取和分析进行简单的介绍,希望能够遇到更多志同道合的可转债投资朋友们。
1. 数据获取
数据获取是进行可转债分析的基础。笔者了解到网络上存在很多能够提供可转债量化分析的网站,但一部分网站需要缴费,因此没有太多的关注。笔者目前主要是通过Akshare(https://akshare.xyz)提供的数据接口下载目前仍在交易的可转债,主要思路是通过一个接口获取可转债的代码,随后调用另一接口获取对应代码的历史交易数据。
代码如下:
df=ak.bond_zh_hs_cov_spot()
code_list=df[['symbol','name']].values
def create_path():
global path
path = os.path.join(".","all_stock_candle","stock")
# 保存数据
if not os.path.exists(path) :
# os.mkdir(path) # 可以建一级文件夹
os.makedirs(path) # 可以建多级文件夹
file_name = symbol ".csv"
return os.path.join(path,file_name)
for symbol,ak_name in code_list[72:]:
print(symbol,ak_name)
if "定" in ak_name:
continue
else:
df = ak.bond_zh_hs_cov_daily(symbol = symbol)
df.sort_values(by=['date'],ascending=True,inplace=True)
df.reset_index(drop=True, inplace=True)
path=create_path()
df.to_csv(path, index=False, mode='w',encoding='gbk')
time.sleep(2)
通过上述操作变能够获取当前所有的在交易的可转债。这一部分数据对于回测分析也是足够的了。另外,有大量可转债由于强赎到期等原因已经退市,想获取更精确的回测过程,可以通过爬虫等方法进一步获取,笔者这里首先是通过宁稳网获取了目前所有已退市的可转债代码,随后通过已退市的代码在集思录官网获取相应的历史数据。通过上述过程便获取了在规定时间内的所有可转债交易数据。
2. 数据的补充和清洗
我们通过上述过程只能够得到目前在交易的可转债信息,如图1所示,缺乏对应的转股溢价率等信息,因此需要进一步的处理。
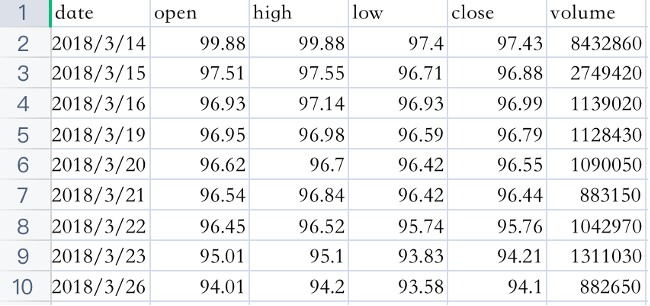
图1. 交易可转债历史行情信息
ak.bond_zh_cov_value_analysis这个接口可以提供可转债转股溢价率等信息,因此需要将上述的两个接口获取的数据进行进一步的结合,便可以得到每只可转债较为完整的历史行情信息,这里最需要注意的是两个接口得到的数据存在停牌期的差异,需要通过一行代码将停牌期的数据删除。另外需要注意的是,我通过另一个接口获取了历史交易日可转债对应正股的流通市值,都在akshare有对应接口调用,不难。所得结果如图2所示,
图2. 增加了转股溢价率等数据的历史行情信息
3. 数据的回测
在获取所有上述所有数据之后,便可以对数据进行回测和分析。这里采用三种最常见的策略,即双低、低溢价和低价策略,回测日期这里以2020年6月1日至2023年11月7日为止,具体的构建矩阵方法可以参看“ 野生交易员的试炼之路”的“20行Python搞定可转债回测”一文作为参考。我们可以选用20只可转债,等权重购买,每日轮换,未考虑摩擦成本,并将可转债等权指数和沪深300指数作为参考,得到如下图的回测结果,可以发现通过低溢价策略能够获取显著的收益率。
图3. 不同可转债策略获取的净值变化图。(20200601-20231107)
改变回测日期,如2022年6月1日至2023年11月7日,获取如图4所示的结果,可以发现仍然是通过低溢价策略能够获取显著的超额收益。
图4. 不同可转债策略获取的净值变化图。(20220601-20231107)
笔者这里选择的可转债数目为20只,对于可转债数目对于净值的影响则做了进一步的分析,回测策略保持一致,得到了如图5的结果,结果表明随着可转债持有数目的增加,可转债的波动率减小,同时当可转债数目大于10只时,总体回报率几乎一致,表明适当增加持仓数目能够提高持仓幸福感同时不减少回报率。
图5. 低溢价策略不同持仓个数净值变化图。(20220601-20231107)
为具体表示这一趋势,我们计算了不同数目时的夏普比,其公式不再累赘,年化回报率取2.315,得到的结果如图6所示。同时我们也计算了最大回撤率,结果如图7所示,从图6和图7的结果可以看出,适当的分散数目能够保证我们在获取相似的回报率同时降低回撤,提高持股感受。
图6. 低溢价策略不同持仓的夏普比率变化。(20220601-20231107)
图7. 低溢价策略不同持仓数目的最大回撤率。(20220601-20231107)
1. 数据获取
数据获取是进行可转债分析的基础。笔者了解到网络上存在很多能够提供可转债量化分析的网站,但一部分网站需要缴费,因此没有太多的关注。笔者目前主要是通过Akshare(https://akshare.xyz)提供的数据接口下载目前仍在交易的可转债,主要思路是通过一个接口获取可转债的代码,随后调用另一接口获取对应代码的历史交易数据。
代码如下:
df=ak.bond_zh_hs_cov_spot()
code_list=df[['symbol','name']].values
def create_path():
global path
path = os.path.join(".","all_stock_candle","stock")
# 保存数据
if not os.path.exists(path) :
# os.mkdir(path) # 可以建一级文件夹
os.makedirs(path) # 可以建多级文件夹
file_name = symbol ".csv"
return os.path.join(path,file_name)
for symbol,ak_name in code_list[72:]:
print(symbol,ak_name)
if "定" in ak_name:
continue
else:
df = ak.bond_zh_hs_cov_daily(symbol = symbol)
df.sort_values(by=['date'],ascending=True,inplace=True)
df.reset_index(drop=True, inplace=True)
path=create_path()
df.to_csv(path, index=False, mode='w',encoding='gbk')
time.sleep(2)
通过上述操作变能够获取当前所有的在交易的可转债。这一部分数据对于回测分析也是足够的了。另外,有大量可转债由于强赎到期等原因已经退市,想获取更精确的回测过程,可以通过爬虫等方法进一步获取,笔者这里首先是通过宁稳网获取了目前所有已退市的可转债代码,随后通过已退市的代码在集思录官网获取相应的历史数据。通过上述过程便获取了在规定时间内的所有可转债交易数据。
2. 数据的补充和清洗
我们通过上述过程只能够得到目前在交易的可转债信息,如图1所示,缺乏对应的转股溢价率等信息,因此需要进一步的处理。

图1. 交易可转债历史行情信息
ak.bond_zh_cov_value_analysis这个接口可以提供可转债转股溢价率等信息,因此需要将上述的两个接口获取的数据进行进一步的结合,便可以得到每只可转债较为完整的历史行情信息,这里最需要注意的是两个接口得到的数据存在停牌期的差异,需要通过一行代码将停牌期的数据删除。另外需要注意的是,我通过另一个接口获取了历史交易日可转债对应正股的流通市值,都在akshare有对应接口调用,不难。所得结果如图2所示,
图2. 增加了转股溢价率等数据的历史行情信息
3. 数据的回测
在获取所有上述所有数据之后,便可以对数据进行回测和分析。这里采用三种最常见的策略,即双低、低溢价和低价策略,回测日期这里以2020年6月1日至2023年11月7日为止,具体的构建矩阵方法可以参看“ 野生交易员的试炼之路”的“20行Python搞定可转债回测”一文作为参考。我们可以选用20只可转债,等权重购买,每日轮换,未考虑摩擦成本,并将可转债等权指数和沪深300指数作为参考,得到如下图的回测结果,可以发现通过低溢价策略能够获取显著的收益率。
图3. 不同可转债策略获取的净值变化图。(20200601-20231107)
改变回测日期,如2022年6月1日至2023年11月7日,获取如图4所示的结果,可以发现仍然是通过低溢价策略能够获取显著的超额收益。
图4. 不同可转债策略获取的净值变化图。(20220601-20231107)
笔者这里选择的可转债数目为20只,对于可转债数目对于净值的影响则做了进一步的分析,回测策略保持一致,得到了如图5的结果,结果表明随着可转债持有数目的增加,可转债的波动率减小,同时当可转债数目大于10只时,总体回报率几乎一致,表明适当增加持仓数目能够提高持仓幸福感同时不减少回报率。
图5. 低溢价策略不同持仓个数净值变化图。(20220601-20231107)
为具体表示这一趋势,我们计算了不同数目时的夏普比,其公式不再累赘,年化回报率取2.315,得到的结果如图6所示。同时我们也计算了最大回撤率,结果如图7所示,从图6和图7的结果可以看出,适当的分散数目能够保证我们在获取相似的回报率同时降低回撤,提高持股感受。
图6. 低溢价策略不同持仓的夏普比率变化。(20220601-20231107)
图7. 低溢价策略不同持仓数目的最大回撤率。(20220601-20231107)
 Edge
Edge Chrome
Chrome Firefox
Firefox







 京公网安备 11010802031449号
京公网安备 11010802031449号