Edge
Chrome
Firefox
前言
今年公司的事情比较多，所以在个人投研上花费的精力较少；这应该是今年最后一篇研究札记了。最近读了一篇发表于2020年10月的论文《Practical Implementation of the Kelly Criterion: Optimal Growth Rate, Number of Trades, and Rebalancing Frequency for Equity Portfolios》，该文综述了学术界在凯利公式方面的相关研究，同时开发了一个通用框架，将凯利准则应用于股票市场数据，从而应用于投资组合优化。随后，我又做了一些相关的简单测算，并将想法记录如下，欢迎讨论交流。
根据我的发帖习惯，还是先给出结论：
1、在现实投资环境中，经典凯利公式的实用性有限 —— 最粗糙的用法是，不要在单一资产或股票上，投入超过50%的总资金。
2、在实际投资环境中，多数情况下，采用凯利公式（变形）和等权重配置，很难说孰优孰劣，但基于稳健性（robust）、参数更少（过拟合的可能更低）和实操难度更低的考虑，我个人更倾向于采用等权重配置、而非凯利公式。
3、在 @账户已注销 的投资框架中，通过凯利公式（变形），可以将“投稳”和“投变”的资产，组合成一个类似于“投增”的资产；“投变”资产的具体配置比例，可以根据个人的偏好，在凯利公式计算结果的50-100%之间滑动。
一、经典凯利公式、变形及风险平价策略
1、经典凯利公式
经典的凯利公式，如下所示；而通过凯利公式计算某一资产的资金配置比例，需要知道 胜率（获胜概率）和 赔率（盈亏比）。PS：关于经典凯利公式的推导过程，可以看 up主 科技3D视界 《凯利公式，以及一个横扫股圈的男人》 ；讲述地非常简洁和容易理解（但需要注意的是，这个up主的其他视频并不是完全正确的，部分内容存在偷换概念和其他问题，观看时请自行甄别）。
2、凯利公式的变形
在现实投资环境中，凯利公式需要的两个参数（胜率与赔率）是比较难精准统计和测算的。如果假设资产价格的波动符合正态分布，那么经典的凯利公式，可以变形为如下所示（具体推导过程，可以参见论文中的公式 9，这里就不详述了）；
同时，所需参数，也由 胜率和赔率，变为 资产收益的均值（u）、资产价格的波动率（σ）和无风险利率（r）；而这3个参数，是比较容易获取和统计的。
3、变形的衍生：风险平价策略
如果假设各类资产的长期夏普比例相同并且无风险利率为0，那么凯利公式（变形）的配置原则就类似于风险平价策略了（波动率大的少配、波动率小的多配）。PS：当然，这是一个粗糙的比喻；事实上，还需要考虑资产间的协方差，如下所示。
这里想说一句题外话：
通过对凯利公式设置新的假设条件和参数，就可以把不同的投资思想串联到一起，这个推导其实是很美的，同时这个过程也很让人享受 —— 就好像当初刚学概率分布的时候，以正态分布为基础，通过调整假设和参数，就可以推导出不同概率的关联图谱，把伯努利分布、二项分布、泊松分布等等，都串联起来。
二、凯利公式（变形）的资金配置原则
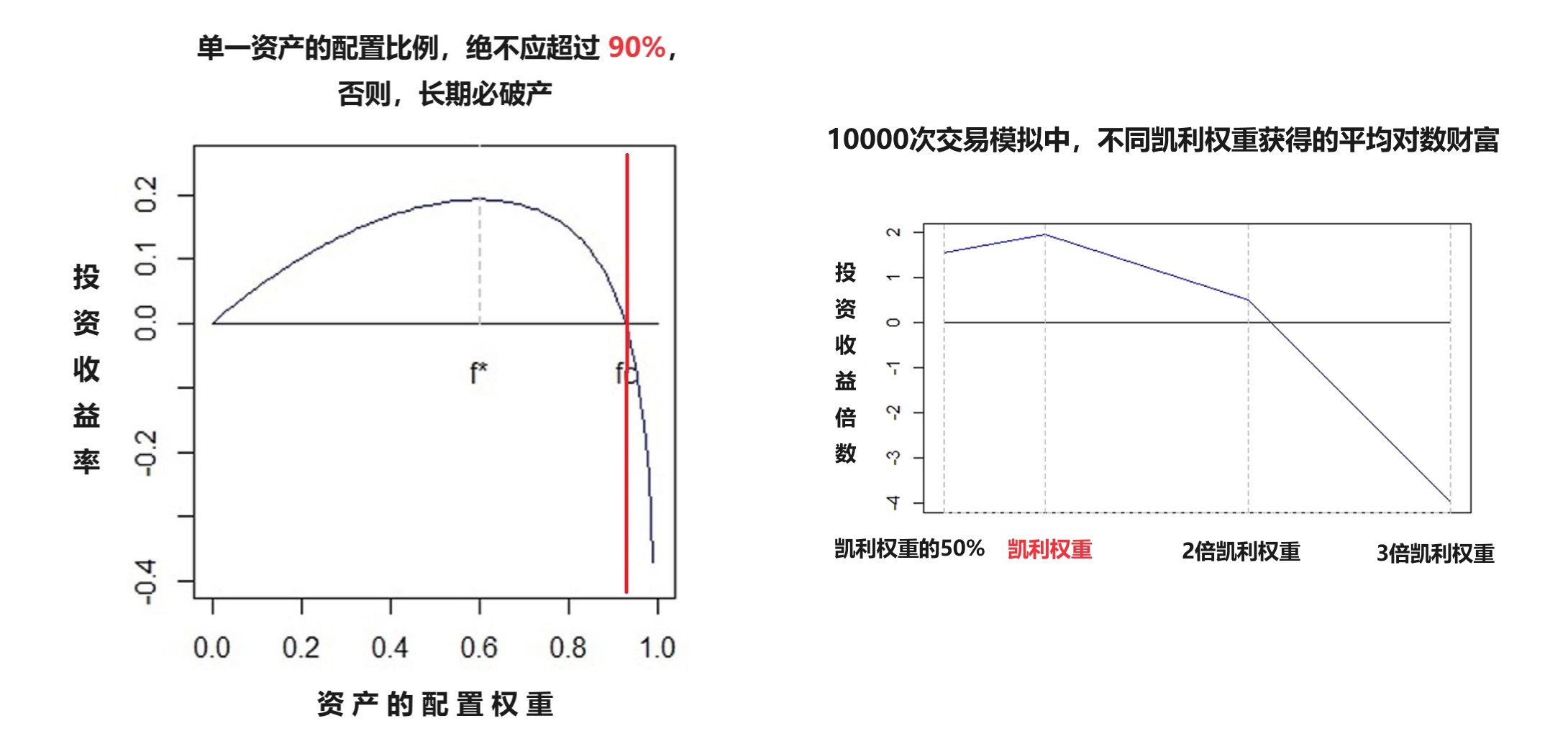
根据上述论文的蒙特卡洛模拟的结果，如下图所示，1）单一资产的配置比例绝不能超过90%（下图的 fc） —— 否则，长期看，终将破产
2）单一资产的配置比例的最优值在[50%, 70%]（下图的 f*）
3）如果投资者偏好相对保守，采用半凯利比例（half-kelly），将单一资产的配置比例设定在[25%-35%]也是可以的。
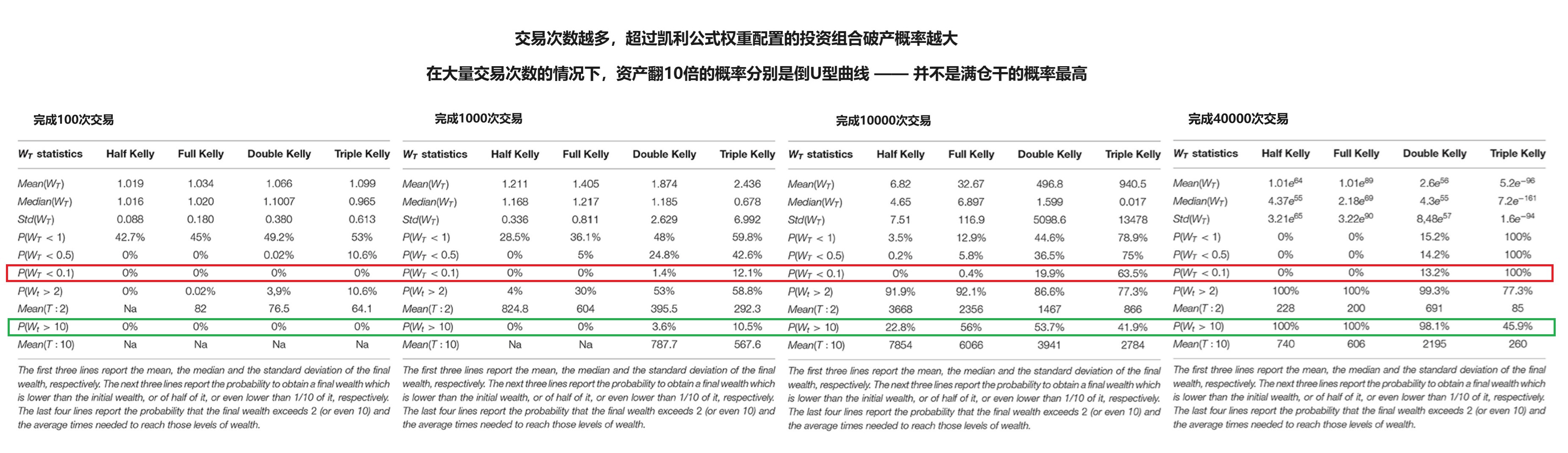
具体的蒙特卡洛模拟结果，可以参见下面的图表：
三、凯利公式（变形）与等权重配置的对比
在下文的对比中，计算凯利公式所需参数时，我采用的是1年的滚动窗口（而不是论文中推荐的2年的滚动窗口）。采用这个参数的原因是，从历史数据看，大类资产均存在较为明显的1年期动量（详情参阅 AQR的论文 《Value and Momentum Everywhere》，这里就不赘述了）。
通过对比下面的3组数据：
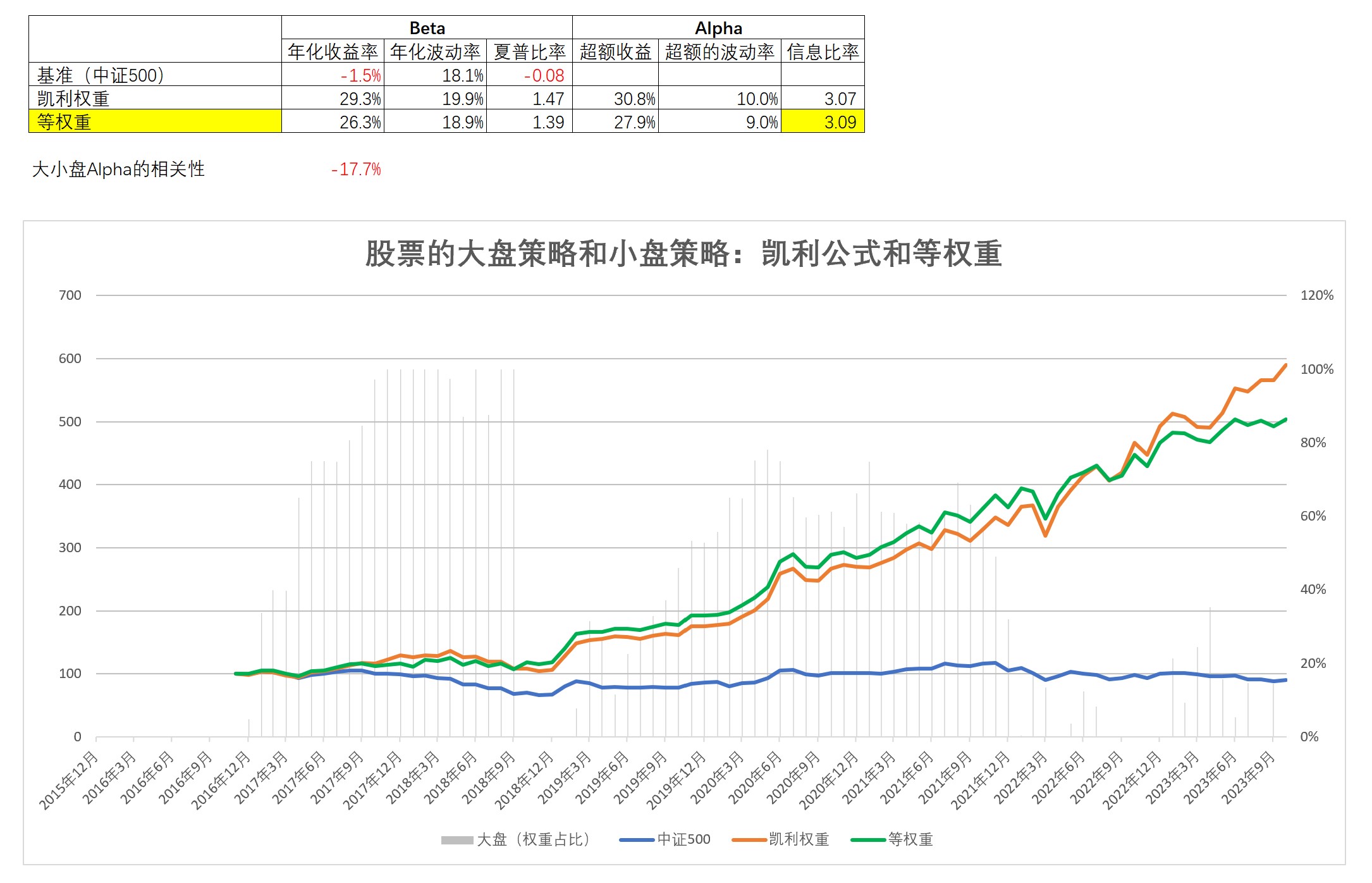
1）A股的大盘量化策略和小盘量化策略
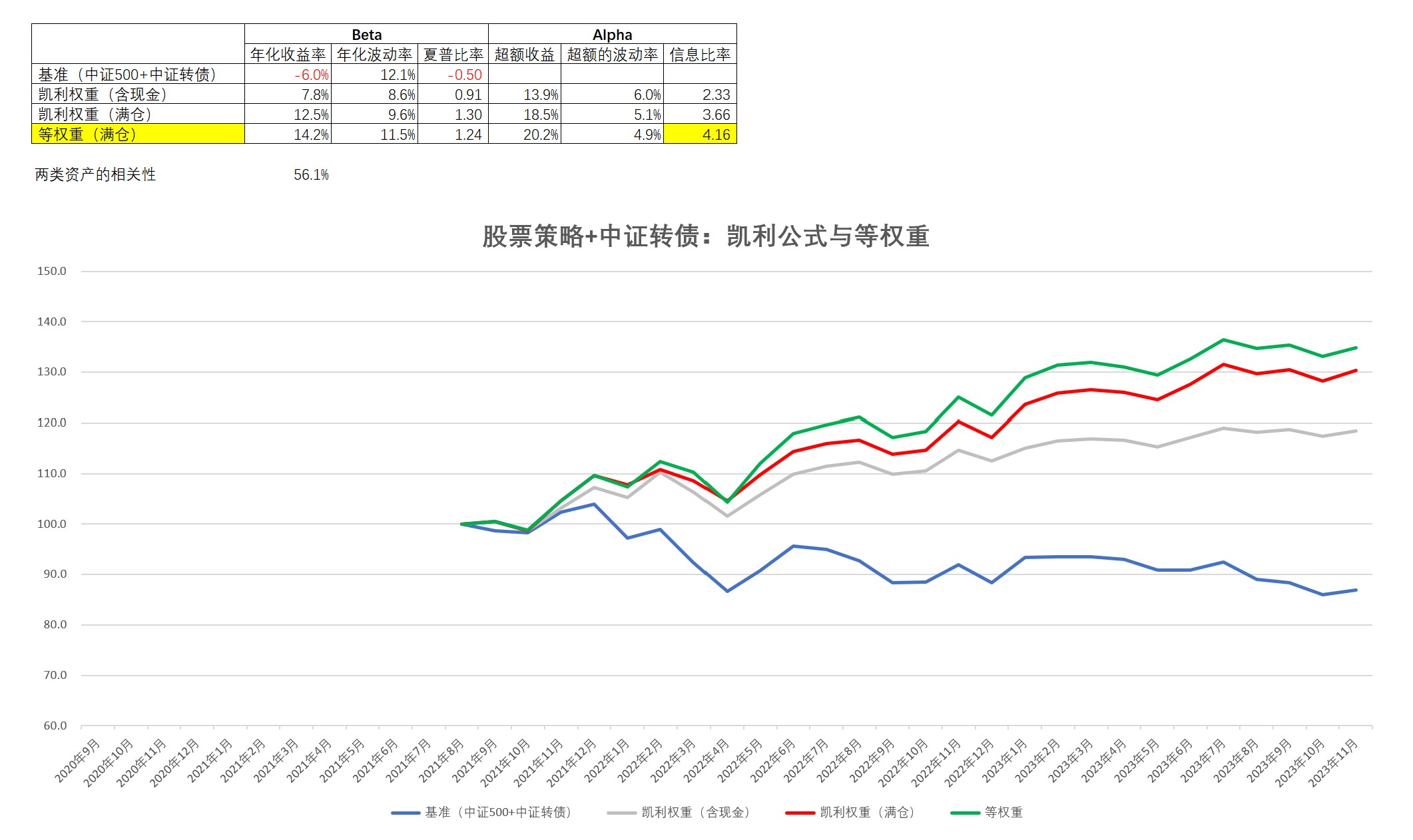
2）A股量化策略和可转债量化策略
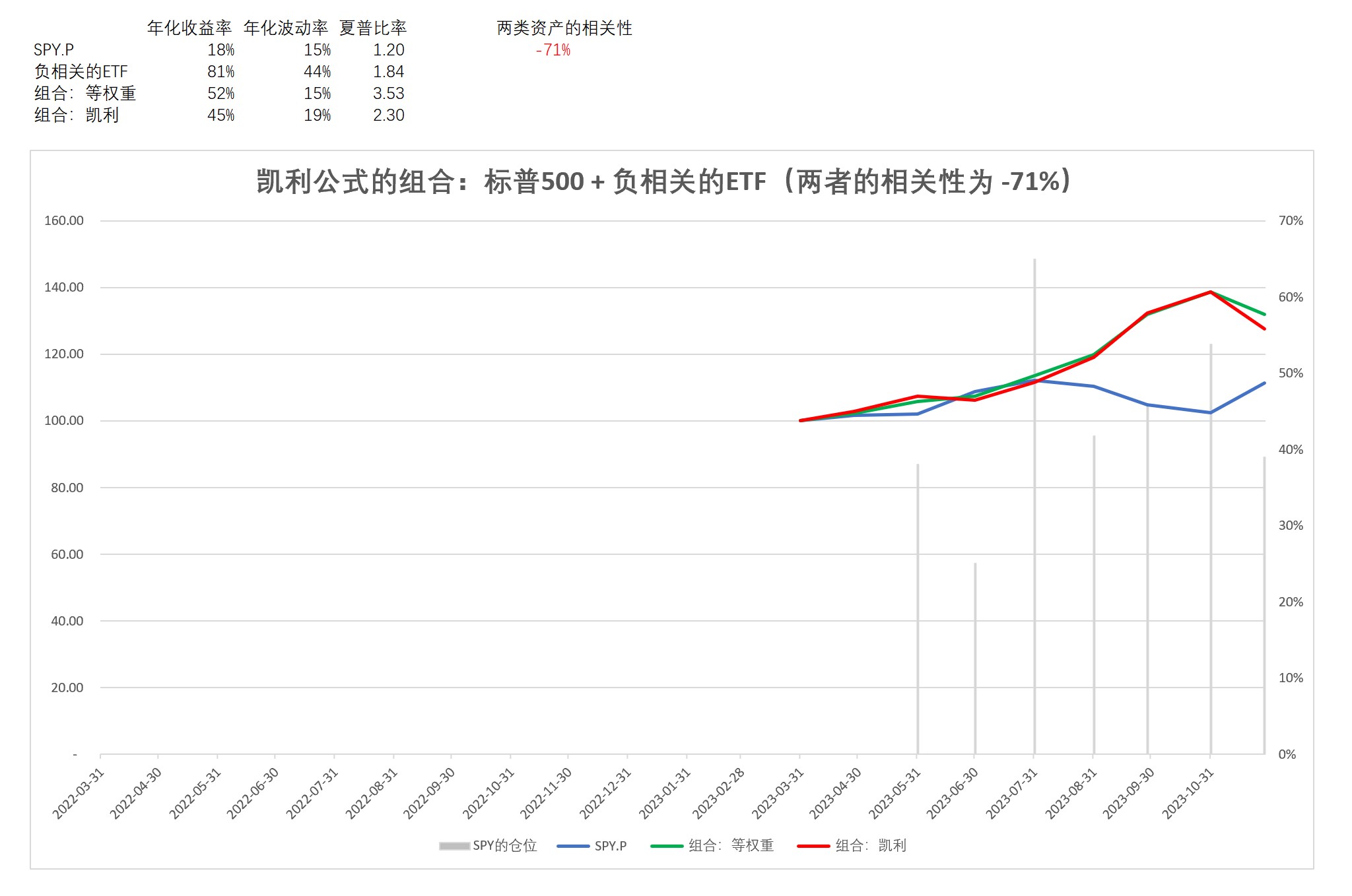
3）标普500和与其高度负相关的资产
可以发现：
1）凯利公式和等权重配置的长期业绩难分伯仲，而在实操上，等权重更为简单
2）资产相关性的高低，对凯利公式的超额影响并不显著，主要原因是我的测算中凯利公式是1阶的，没有考虑2阶问题。
四、用“投稳”+“投变”拟合出“投稳”
@账户已注销 的投资框架中，投稳 30%、投变 10%、投增 60%。其中，“投稳”主要投向类现金资产；“投变”主要投向可能增长10倍、100倍，但也可能归零的高风险、高波动标的；“投增”主要是投向“四猛”行业。
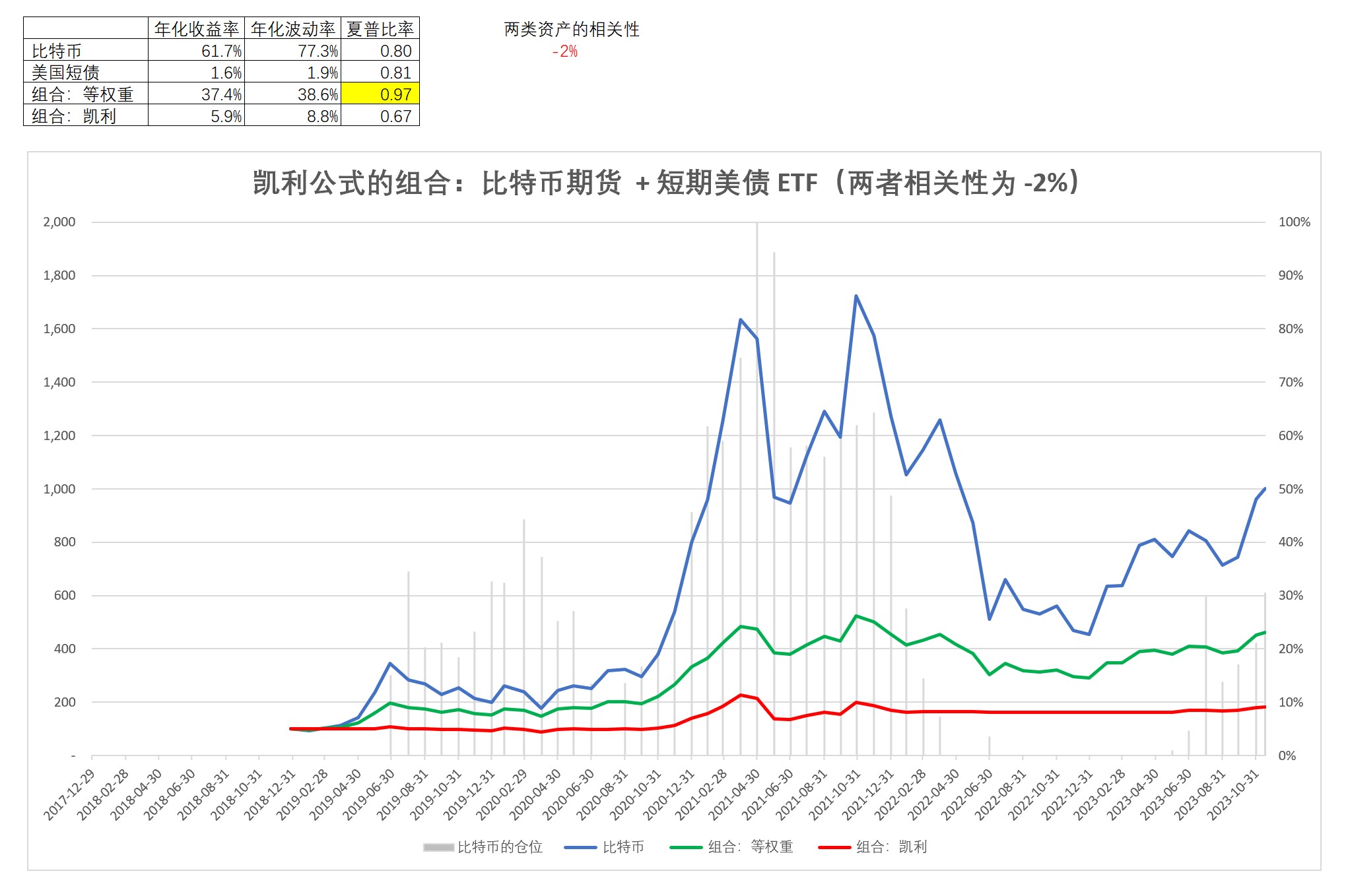
如果用比特币作为“投变”资产、美国短期国债作为“投稳”资产，那么
1）采用等权重配置+月度再平衡，可以获得类似高风险股票的收益
2）采用凯利公式（变形）配置+月度再平衡，可以获得类似于高等级信用债的收益
详情参见下图：
因此，投资者可以根据自己的风险偏好，在凯利公式和等权重比例之间，主动定制自己投资组合的整体预期收益和回撤风险 —— 这也是凯利公式带给我们的核心思想。
五、几种杠杆工具和凯利公式的组合使用
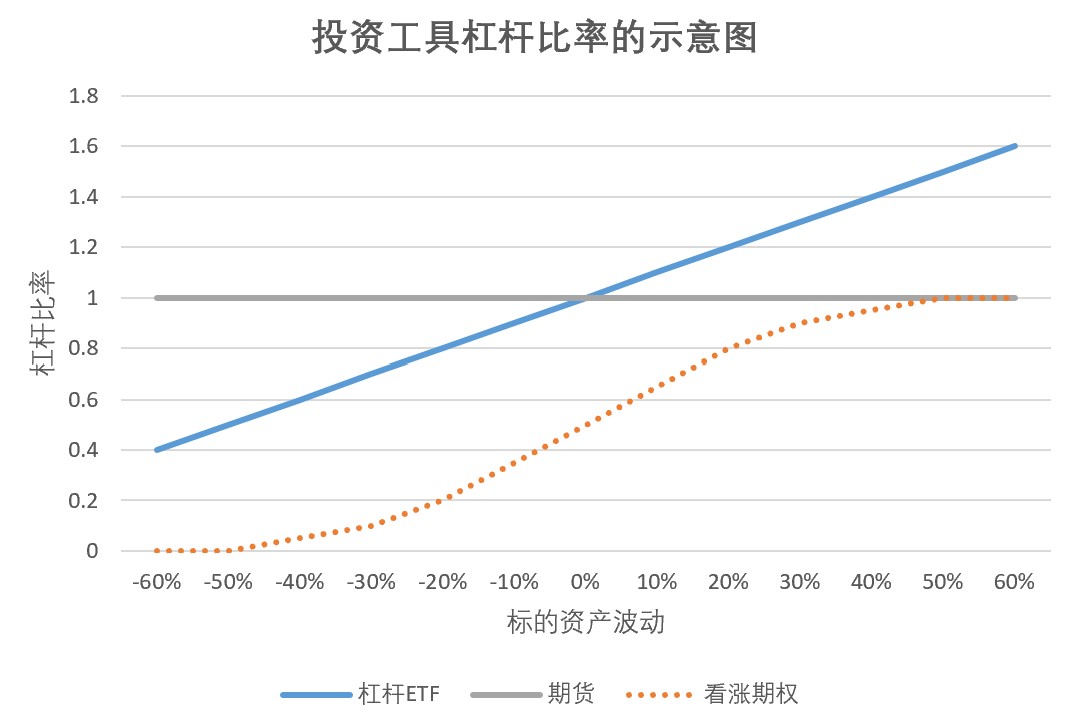
这部分就不展开了，因为说起来比较麻烦；但是仍然欢迎有兴趣的网友一起讨论。在《牛年薄献，普通人可学可用的反脆弱风险控制理念和实践》的回帖中，我给出了不同杠杆的Beta变化情况，如下图所示：
PS：下面的图，是基于期货的Beta始终为1作为参照系的；如果把参照系改成是杠杆ETF始终为1，那么对应的图表是需要变形的。
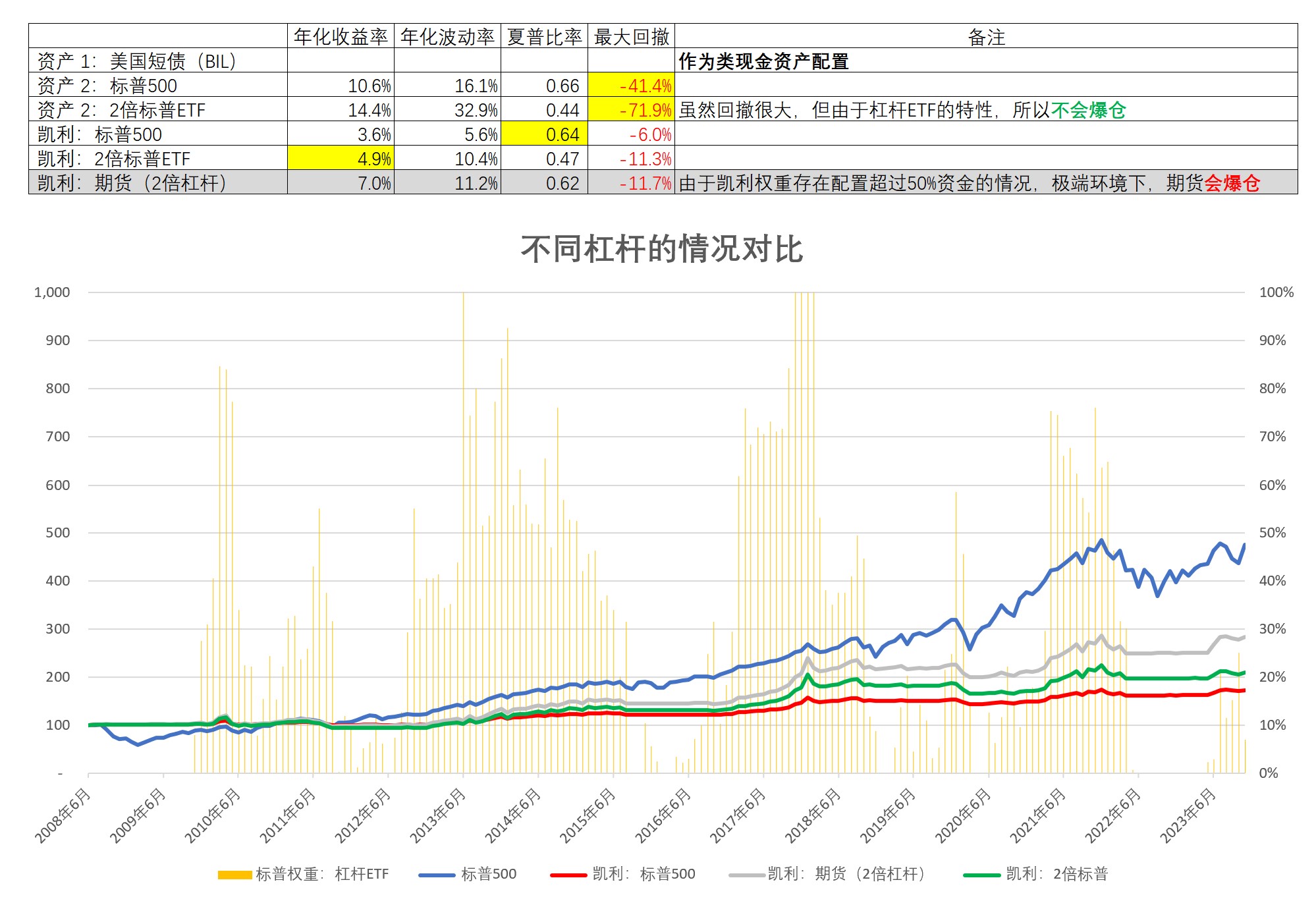
然后，把这些杠杆工具和凯利公式组合使用，在美国市场上，可以得到下面的图表。
六、结论
1、凯利公式，给出了大的资金管理原则；至于具体的参数细节，则不用过于纠结。2、对于像我这样的懒人来说，等权重配置也挺好。
3、通过“投稳”和“投变”这两类差异极大的资产，结合凯利公式，就可以构建出稳健的“哑铃型”投资组合。
4、杠杆工具和资金配置的组合使用，是可以继续深入研究的 ——“九债一购”是思想框架，是用于启发的，而不是用于“恪守”的。
10
赞同来自: 不啻微茫 、Luff123D 、zddd10 、wangcaidu 、topdeck 、 、 、 、 、更多 »
@zhouxinyu19
首先，等权重配置的普适性比较强；在绝大多数的市场和情况下，都是次优解。具体的数据和统计，可以去知乎上找找石川的相关文章（例如，《如何分配资金？组合优化的是是非非》）。
其次，等权重配置，只有1个参数（有几个资产，N=几），所以，过拟合的可能性比较低。
最后，就是计算和操作的简单省心；不用历史数据、不用算波动率（最小方差等）。
所以，总的来说，在自身认知有限、甚至无知的情况下（没有现实逻辑可靠的切换方法之前），等权重都是很好的应对方案。
另外，说到等权重配置，我总是想起金庸《侠客行》里面的一个例子：
大神能否详细聊聊等权重配置？等权重，挺好的；我自己也在用。
首先，等权重配置的普适性比较强；在绝大多数的市场和情况下，都是次优解。具体的数据和统计，可以去知乎上找找石川的相关文章（例如，《如何分配资金？组合优化的是是非非》）。
其次，等权重配置，只有1个参数（有几个资产，N=几），所以，过拟合的可能性比较低。
最后，就是计算和操作的简单省心；不用历史数据、不用算波动率（最小方差等）。
所以，总的来说，在自身认知有限、甚至无知的情况下（没有现实逻辑可靠的切换方法之前），等权重都是很好的应对方案。
另外，说到等权重配置，我总是想起金庸《侠客行》里面的一个例子：
丁不四双掌转了几个弧形，斜斜拍出，这一招叫做‘或左或右’，掌力击左还是击右，要看当时情景而定，心头暗喜：“臭小子，这一次你可不能照抄了吧？你怎知我掌力从那一个方向袭来？”果然石破天见这一招难以仿效，问道：“你是攻左还是攻右？”丁不四一声狂笑，喝道：“你倒猜猜看！”两只手掌不住颤动。石破天心下惊怕，只得提起双掌，同时向丁不四掌上按去，他不知对方掌力来自何方，惟有左右同时运劲。丁不四见他双掌一齐按到，不由得大惊，暗想傻小子把这招虚中套实、实中套虚的巧招使得笨拙无比，‘或左或右’变成了‘亦左亦右’，两掌齐重，令此招妙处全失。所以，市场总是“或左或右”，而“亦左亦右”的笨办法却可以使其“妙处全失” —— 等权重配置，就是这个笨办法、是次优解（最优解，当然是你能够明确判断是左还是右、但这个难度就一下子提高了很多，不是“无知”可以赚的钱）。
34
赞同来自: topdeck 、zengyongqiang 、精神科王主任 、好奇心135 、well向前冲 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、更多 »
现实世界中，凯利公式应用范围非常有限。
原因有两点：
1、盈亏问题。你每投出一份资金，并不像买彩票或赌博筹码那样要么输掉筹码，要么按一定赔率盈利。现实情况是，投进去的资金有可能亏10%，也可能亏50%，或则盈利20%，或则不亏不赚。
2、期限问题。买彩票或上赌桌，你知道这一局什么时候结束。但现实投资不是这样，你买入一支股票，究竟什么时候达到预期结束投资，事先是不知道的。
基于此，凯利公式在现实投资活动中，无法量化公式中的两个关键变量b、p，也就限制了公式的实际应用。
原因有两点：
1、盈亏问题。你每投出一份资金，并不像买彩票或赌博筹码那样要么输掉筹码，要么按一定赔率盈利。现实情况是，投进去的资金有可能亏10%，也可能亏50%，或则盈利20%，或则不亏不赚。
2、期限问题。买彩票或上赌桌，你知道这一局什么时候结束。但现实投资不是这样，你买入一支股票，究竟什么时候达到预期结束投资，事先是不知道的。
基于此，凯利公式在现实投资活动中，无法量化公式中的两个关键变量b、p，也就限制了公式的实际应用。
6
赞同来自: 流沙少帅 、明青 、well向前冲 、巴兰 、吉吉木 、更多 »
@ylxwyj
另外后面那一大段关于凯利公式与夏普之间的区别。我这还是没有详细计算，但还是有直觉：凯利虽然明面上考虑的是长期期望收益，但其实也是考虑了波动的。比如就凯利来说，两个策略，年化收益都是20%，但是波动一个年化10%，一个20%，明显前者的仓位要大一些。所以凯利和夏普之间关于波动与收益之间的关系可能只是系数不一样？（我不确定，还是年底有空来详细研究下）
1）这个调仓周期的影响，我不清楚。我是按自己的习惯，用的月度调仓。怎么说呢，杠杆其实就是放开100%后广义的仓位。只有优秀的策略才谈得上杠杆，所以我觉得没必要被广义普通资产的夏普限制住（一般在0.3，比较好的是0.5比如标普，再好点估计是巴菲特了0.7）。年底希望有时间能研究下广义的杠杆取多少。其实用个简单的例子来说，如果现在IC年化贴水是30%，直觉上我认为集思录很多人压迫上1倍杠杆（甚至还偏少了），那么实际应该上多少杠杆呢？用你第二个公式的话，肯定是要上杠杆的。
2）你这个100%不爆仓的前提，其实是隐含了假设股指这个资产本身不会破产归零。
但是，在蒙特卡洛模拟里面，其实是不包含这个假设的。极端的例子，可以想一下中华民国时期（1911-1949）的股市，已经爆仓的各种币、P2P、信托产品，也可以是买彩票。
嗯，夏普高于1，其实是很优秀的策略了，或者说是某个资产涨幅最好的一段时间了。
如果考...
另外后面那一大段关于凯利公式与夏普之间的区别。我这还是没有详细计算，但还是有直觉：凯利虽然明面上考虑的是长期期望收益，但其实也是考虑了波动的。比如就凯利来说，两个策略，年化收益都是20%，但是波动一个年化10%，一个20%，明显前者的仓位要大一些。所以凯利和夏普之间关于波动与收益之间的关系可能只是系数不一样？（我不确定，还是年底有空来详细研究下）
6
赞同来自: 好奇心135 、newsu 、zhuqi123456 、巴兰 、dhhlys 、更多 »
@dhhlys
2）你这个100%不爆仓的前提，其实是隐含了假设股指这个资产本身不会破产归零。
但是，在蒙特卡洛模拟里面，其实是不包含这个假设的。极端的例子，可以想一下中华民国时期（1911-1949）的股市，已经爆仓的各种币、P2P、信托产品，也可以是买彩票。
如果考虑普遍情况的话，大类资产的长期收益率大致在0.3左右，所以，整体看，这个假设是没什么问题的。
其实，在paper的原文里面就提到了（参见下图），凯利公式的配置权重，不在有效边界的切线上 —— 它放弃了最高的夏普比例，而是选择了更高的收益、同时也承担了更更高的风险。
这个思路的区别，就好像同样做股票量化策略，我选择不用股指期货对冲、承担Beta风险；而泛舟Rain会用股指期货对冲，规避Beta风险。假设我们两者的alpha能力相同，在实际投资中，从长期来看，大概率我的投资组合的收益可能更高一点（因为即使是A股，Beta也是有缓慢增长的），但同时我承受的波动会更更大 —— 在“不死”的前提下，我（Kelly）愿意承担更更大的波动、去最求更高的收益，即使风险回报比不是最高的、但是绝对值最高就行。
其实，关于马科维茨，我最不信任的一点就是covariance的稳定性和持续性；如果这点不成立，理论很美好，实际效果可能就比较哈哈。 嗯，我宁愿选择相信 trend/momentum，也不会选择相信 covariance。
另外，还有一个我印象比较深刻的例子，戴维斯文森在《机构投资的创新之路》里面举过一个例子，1970年代的某年，他们算出来一个资产配置比例，然后又人为拍脑袋给了一个比例，两者相差巨大（书中有表格）；最后，他们选择了拍脑袋的那个，并取得了良好收益。真是呵呵了~
2013年，JPM发过一个研报《Systematic Strategies Across Asset Classes
Risk Factor Approach to Investing and Portfolio Management》，里面就对比过马科维茨（MVO）、等权重（EW）和其他一些权重配置策略（详情如下）。
在无法自由加杠杆的前提下，MVO其实并不是那么吸引人。
第一，根据凯利公式的用法跟调仓周期有关，如果按照日调仓的话，并且100%仓位，甚至150%爆仓其实是不可能的（以年华15%，年华波动率20%然后用根号下标准差化到日）。或者说长期满仓（不加杠杆）吃贴水，是不可能爆仓的。1）这个调仓周期的影响，我不清楚。我是按自己的习惯，用的月度调仓。
2）你这个100%不爆仓的前提，其实是隐含了假设股指这个资产本身不会破产归零。
但是，在蒙特卡洛模拟里面，其实是不包含这个假设的。极端的例子，可以想一下中华民国时期（1911-1949）的股市，已经爆仓的各种币、P2P、信托产品，也可以是买彩票。
第二，第二部分那个公式推导我看过，它正太推倒的时候做了一个强假设：收益远小于波动。对于优秀的策略来说这个站不住脚。嗯，夏普高于1，其实是很优秀的策略了，或者说是某个资产涨幅最好的一段时间了。
如果考虑普遍情况的话，大类资产的长期收益率大致在0.3左右，所以，整体看，这个假设是没什么问题的。
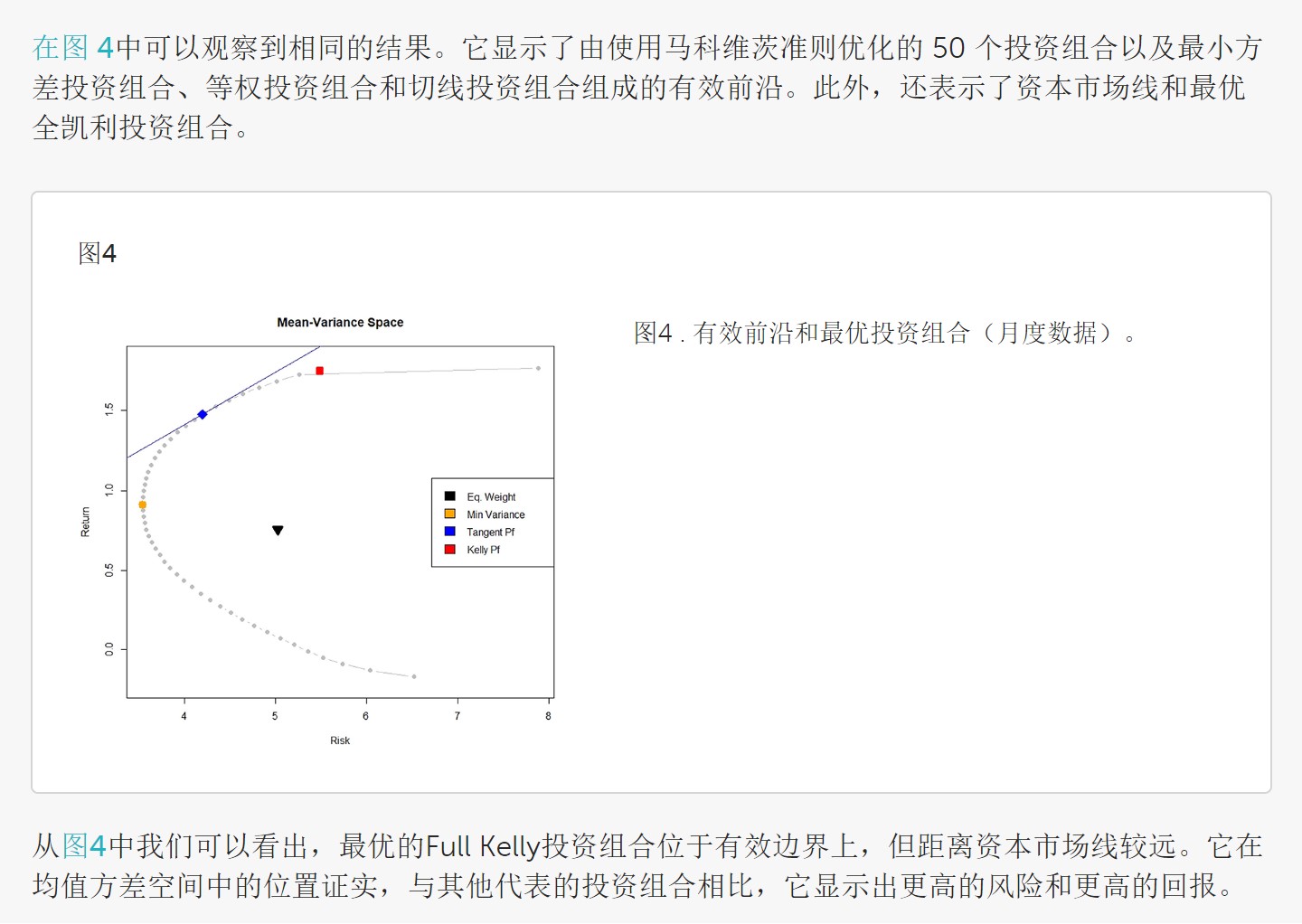
最后跟凯里公式结合属于降维打击，这部分在证券投资学里面有讲，其实就是找夏普最大的切线，然后根据凯利公式（风险偏好）上仓位。这个还真不是这样的。
其实，在paper的原文里面就提到了（参见下图），凯利公式的配置权重，不在有效边界的切线上 —— 它放弃了最高的夏普比例，而是选择了更高的收益、同时也承担了更更高的风险。
这个思路的区别，就好像同样做股票量化策略，我选择不用股指期货对冲、承担Beta风险；而泛舟Rain会用股指期货对冲，规避Beta风险。假设我们两者的alpha能力相同，在实际投资中，从长期来看，大概率我的投资组合的收益可能更高一点（因为即使是A股，Beta也是有缓慢增长的），但同时我承受的波动会更更大 —— 在“不死”的前提下，我（Kelly）愿意承担更更大的波动、去最求更高的收益，即使风险回报比不是最高的、但是绝对值最高就行。
其实，关于马科维茨，我最不信任的一点就是covariance的稳定性和持续性；如果这点不成立，理论很美好，实际效果可能就比较哈哈。 嗯，我宁愿选择相信 trend/momentum，也不会选择相信 covariance。
另外，还有一个我印象比较深刻的例子，戴维斯文森在《机构投资的创新之路》里面举过一个例子，1970年代的某年，他们算出来一个资产配置比例，然后又人为拍脑袋给了一个比例，两者相差巨大（书中有表格）；最后，他们选择了拍脑袋的那个，并取得了良好收益。真是呵呵了~
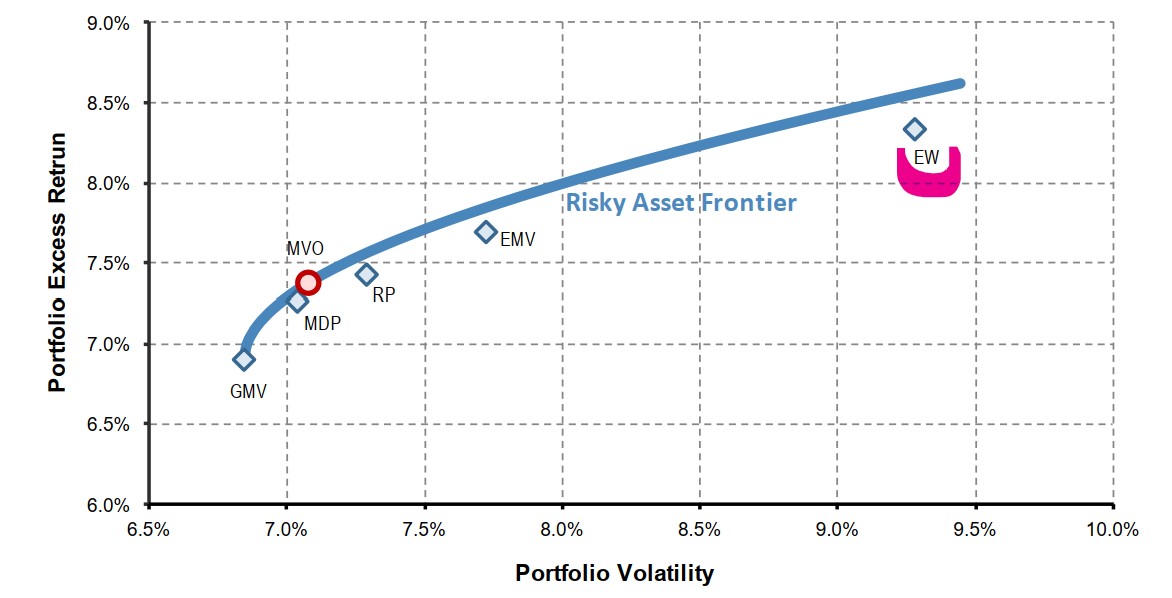
2013年，JPM发过一个研报《Systematic Strategies Across Asset Classes
Risk Factor Approach to Investing and Portfolio Management》，里面就对比过马科维茨（MVO）、等权重（EW）和其他一些权重配置策略（详情如下）。
在无法自由加杠杆的前提下，MVO其实并不是那么吸引人。
0
我怎么觉得结论有问题。
第一，根据凯利公式的用法跟调仓周期有关，如果按照日调仓的话，并且100%仓位，甚至150%爆仓其实是不可能的（以年华15%，年华波动率20%然后用根号下标准差化到日）。或者说长期满仓（不加杠杆）吃贴水，是不可能爆仓的。
第二，第二部分那个公式推导我看过，它正太推倒的时候做了一个强假设：收益远小于波动。对于优秀的策略来说这个站不住脚。
最后其实注销的配置大法本质上还是马克位子组合那套，最后打包起来合成了一个大策略。这个大策略通过分散（投稳投增投变）实现了不降低收益的情况下降低了风险。最后跟凯里公式结合属于降维打击，这部分在证券投资学里面有讲，其实就是找夏普最大的切线，然后根据凯利公式（风险偏好）上仓位
第一，根据凯利公式的用法跟调仓周期有关，如果按照日调仓的话，并且100%仓位，甚至150%爆仓其实是不可能的（以年华15%，年华波动率20%然后用根号下标准差化到日）。或者说长期满仓（不加杠杆）吃贴水，是不可能爆仓的。
第二，第二部分那个公式推导我看过，它正太推倒的时候做了一个强假设：收益远小于波动。对于优秀的策略来说这个站不住脚。
最后其实注销的配置大法本质上还是马克位子组合那套，最后打包起来合成了一个大策略。这个大策略通过分散（投稳投增投变）实现了不降低收益的情况下降低了风险。最后跟凯里公式结合属于降维打击，这部分在证券投资学里面有讲，其实就是找夏普最大的切线，然后根据凯利公式（风险偏好）上仓位
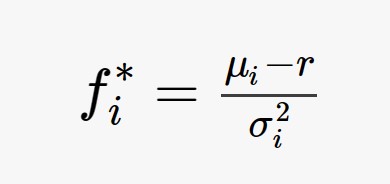
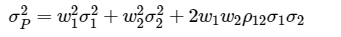
京公网安备 11010802031449号